Question

радиус окружности описанной около правильного треугольника равен 18 найдите высоту этого треугольника

Answer 1

Ответ: 27

Объяснение:

Радиус описанной окружности: R = a/√3. Выразим сторону правильного треугольника:

a = R√3   ⇒   a = 18√3

У правильного треугольника все стороны равны, т.е.

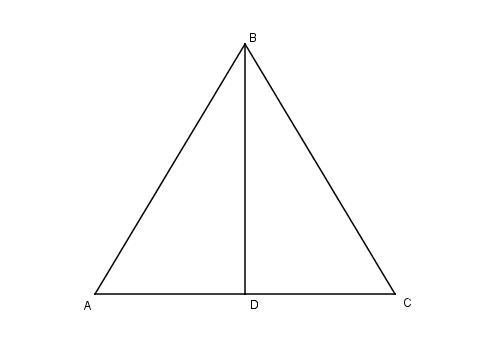
AB = BC = AC = 18√3;  BD - высота; AD = CD = AC/2 = 9√3

Из прямоугольного треугольника ABD по т. Пифагора:

$BD=\sqrt{AB^2-AD^2}=\sqrt{18^2\cdot 3-9^2\cdot3}=27$

Answer 2

Радиус описанной около треугольника окружности связан со стороной треугольника формулой а₃=2R*sin60°=2*18√3/2=18√3

Высота в правильном треугольнике равна а√3/2, значит, высота составляет 18√3*√3/2=9*3=27