Предмет: Алгебра,
автор: annnnna97
ребятки, помогите пожалуйста!
Приложения:
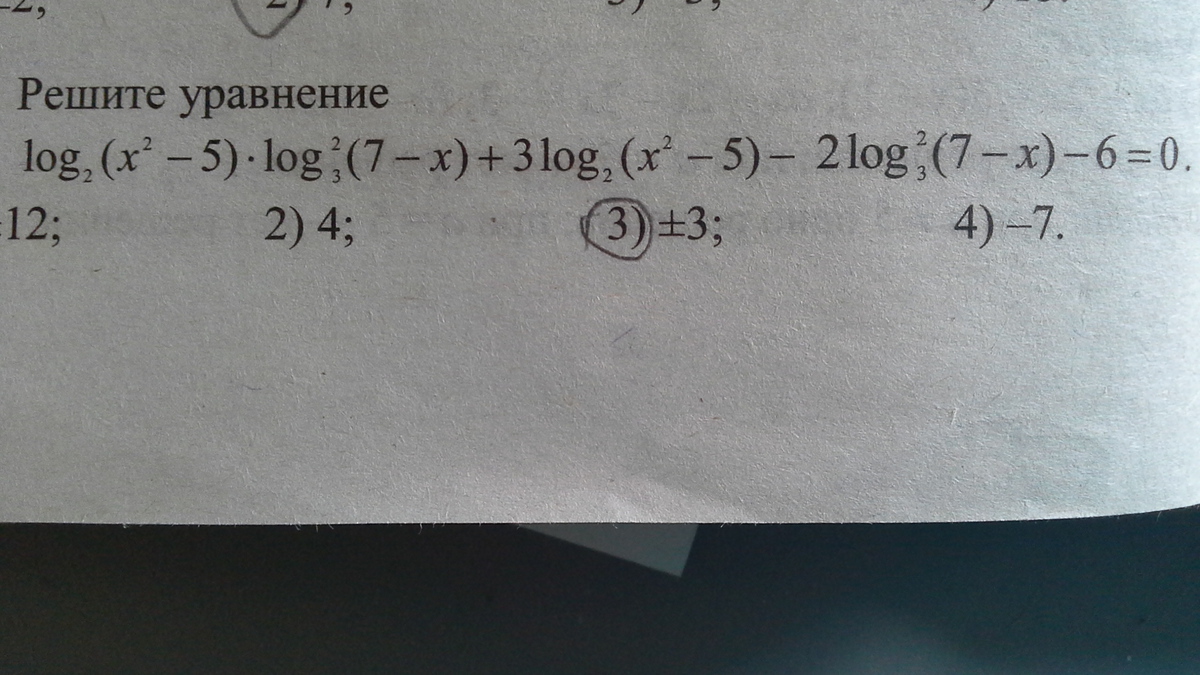
Ответы
Автор ответа:
1
ОДЗ:
Пусть
Обратная замена
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: matvey123pro
Предмет: Русский язык,
автор: olghaasanova
Предмет: Русский язык,
автор: 79409604905
Предмет: Математика,
автор: skime19
Предмет: Химия,
автор: nickolay21