Предмет: Математика,
автор: Аноним
Помогите решить неравенство, пожалуйста!
Приложения:
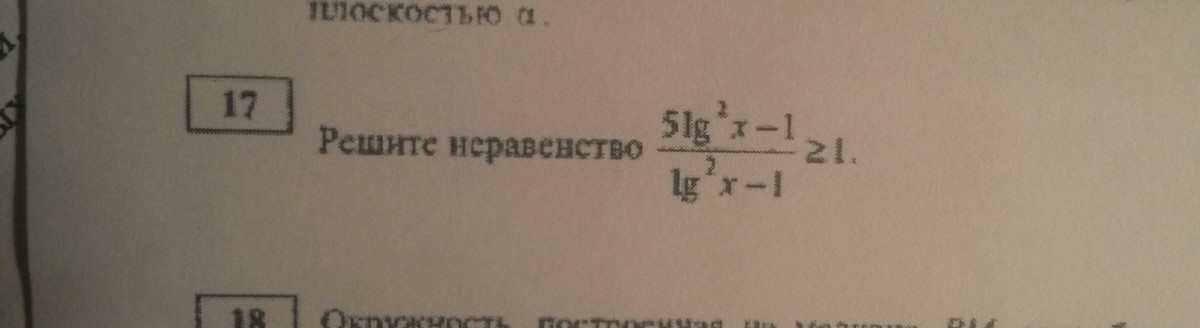
Ответы
Автор ответа:
1
(5lg²x-1)/(lg²x-1)≥1
(5lg²x-1)/(lg²x-1)-1≥0
к общему знаменателю:
(5lg²x-1)/(lg²x-1)-(lg²x-1)/(lg²x-1)≥0
(5lg²x-1-lg²x+1)/(lg²x-1)≥0
(4lg²)/(lg²x-1)≥0
{4lg²x≥0 {lg²x≥0
lg²x-1>0 (lgx-1)(lgx+1)>0
+ - - +
---------------|-------------|------------|---------------- lgx
-1 0 1
{lgx<-1
lgx>1
1. lgx<-1 2. lgx>1
-1=lg10⁻¹=lg(1/10) 1=lg10
lgx<lg(1/10) lgx>lg10. основание 10>1. знак не меняем
{x<(1/10) {x>10
x>0 x>0
ответ: х∈(0;1/10)U(10;∞)
(5lg²x-1)/(lg²x-1)-1≥0
к общему знаменателю:
(5lg²x-1)/(lg²x-1)-(lg²x-1)/(lg²x-1)≥0
(5lg²x-1-lg²x+1)/(lg²x-1)≥0
(4lg²)/(lg²x-1)≥0
{4lg²x≥0 {lg²x≥0
lg²x-1>0 (lgx-1)(lgx+1)>0
+ - - +
---------------|-------------|------------|---------------- lgx
-1 0 1
{lgx<-1
lgx>1
1. lgx<-1 2. lgx>1
-1=lg10⁻¹=lg(1/10) 1=lg10
lgx<lg(1/10) lgx>lg10. основание 10>1. знак не меняем
{x<(1/10) {x>10
x>0 x>0
ответ: х∈(0;1/10)U(10;∞)
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: kristimilafffka
Предмет: Английский язык,
автор: sufle123
Предмет: Математика,
автор: yulia104729
Предмет: Алгебра,
автор: karinaleonteva02