Предмет: Математика,
автор: Erika2323
1.зробіть і поясніть як робити

Варіанти відповідей:1)-1, 2)1, 3)-1,1.
2.Перпендикуляр проведений з точки перетину діагоналей ромба до його сторони,ділить її на відрізки завдовшки 4 см і 25 см.Знайдіть площу ромба.
Варіанти відповідей:1)100 см2, 2)450 см2, 3)580 см2_
Ответы
Автор ответа:
3
Відповідь: х=1
Діагоналі ромба ділять ромб на чотири одинакові прямокутні трикутники, тому площу ромба можна знайти вирахувавши площу одного з трикутників і помножити його на чотири, тобто знайшовши площу усіх цих чотирьох трикутників.
Розглянемо трикутник AOB
Оскільки квадрат висоти прямокутного трикутника, проведеної до гіпотенузи, дорівнює добутку проекцій катетів на гіпотенузу, то
Площа трикутника дорівнює половині добутку довжини сторони трикутника на довжини висоти проведеної до цієї сторони
Приложения:
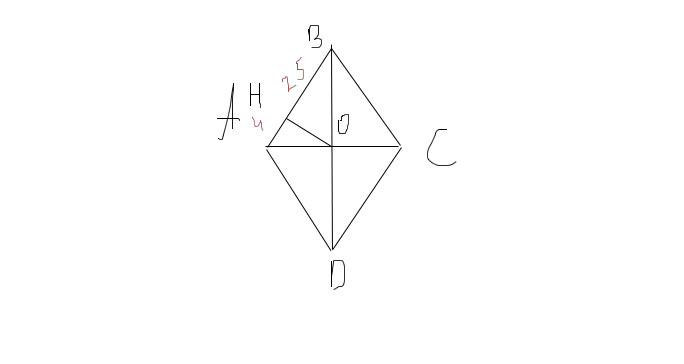
Похожие вопросы
Предмет: Русский язык,
автор: оганрлреппори
Предмет: Английский язык,
автор: Вероника564
Предмет: Қазақ тiлi,
автор: адина58
Предмет: Химия,
автор: ilyaneizvestno10
Предмет: Математика,
автор: iralgajd