Предмет: Геометрия,
автор: kray123
На ребре AA1 прямоугольного параллелепипеда ABCDA1B1C1D1 взята точ- ка E так,
что A1E : EA = 5 : 3, на ребре BB1 - точка F так, что B1F : FB = 5 : 11, а точка
T - середина ребра B1C1. Известно, что AB = 6√2, AD = 10, AA1 = 16.
а) Докажите, что плоскость EFT проходит через вершину D1. б) Найдите площадь сечения
параллелепипеда плоскостью EFT .
Ekaterina1819:
Под цифрой 1 прислать?
да
Сейчас, я немного во 2 напишу, можт поможет чем
ок
Ответы
Автор ответа:
33
Получится вот так :)
Приложения:


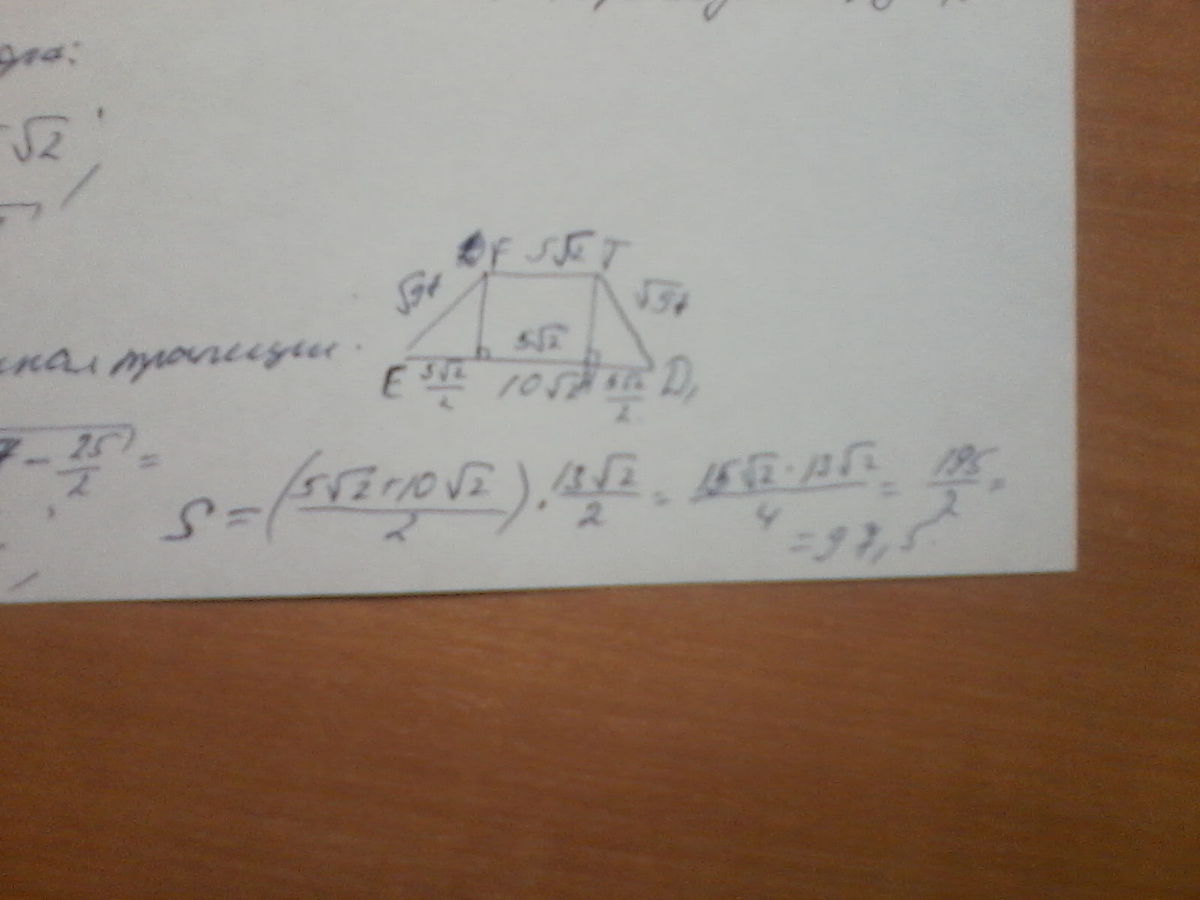
Автор ответа:
16
EA₁ =5/8*AA₁ = 5/8*16 = 10 = A₁D₁ ;
FB₁ =5/16*BB₁ =5/16*16 =5 =B₁T ;
FT | | ED₁
FT = 5√2 ;
ED₁ =10√2 .
D₁T =√((6√2)² +5²)=√97;
проведем FK || A₁B₁ ; K∈ AA₁ ;<FKE =90°;
EF=√(KF² +KE²) =√(A₁B₁²+(A₁E-B₁F)²) ;
EF =√((6√2)² +(10-5)²) =√97 ;
Показали , что ED₁TF равнобедренная трапеция основаниями
ED₁ =10√2 и TF =5√2 ;
ребрами EF = D₁T =√97.
h=√(√97² -(5√2/2)² =13/√2;
S(ED₁TF) =(10√2+5√2)/2*)*13/√2 =15*13/2 =195/2=97,5.
FB₁ =5/16*BB₁ =5/16*16 =5 =B₁T ;
FT | | ED₁
FT = 5√2 ;
ED₁ =10√2 .
D₁T =√((6√2)² +5²)=√97;
проведем FK || A₁B₁ ; K∈ AA₁ ;<FKE =90°;
EF=√(KF² +KE²) =√(A₁B₁²+(A₁E-B₁F)²) ;
EF =√((6√2)² +(10-5)²) =√97 ;
Показали , что ED₁TF равнобедренная трапеция основаниями
ED₁ =10√2 и TF =5√2 ;
ребрами EF = D₁T =√97.
h=√(√97² -(5√2/2)² =13/√2;
S(ED₁TF) =(10√2+5√2)/2*)*13/√2 =15*13/2 =195/2=97,5.
Похожие вопросы
Предмет: Английский язык,
автор: Котя333
Предмет: Другие предметы,
автор: ainurkhazeev08
Предмет: Английский язык,
автор: ДанилаТрояненко
Предмет: Математика,
автор: ruzikk
Предмет: Математика,
автор: Poli1771