Предмет: Геометрия,
автор: rysvlad
Дан ромб ABCD. точка О -точка персечения диогоналей.OС - диаметр окружности. Точка Т - точка пересечения окружности с ромбом на стороне ВС. ВТ=√3(см), а
расстояние от точки О до стороны ромба равно 3(см). Найти радиус и площадь сегментов не входящих в робм.
Формула площади сегмета: Sсегм.=Sсект.-Sвнутри сект. Треугольника.
Формула площади сектора: S =(πr^2)/(360°)*a; где a – градусная мера сектор;
Формула площади треугольника по теореме Виета: S=√(p(p-a)(p-b)(p-c)
Приложения:
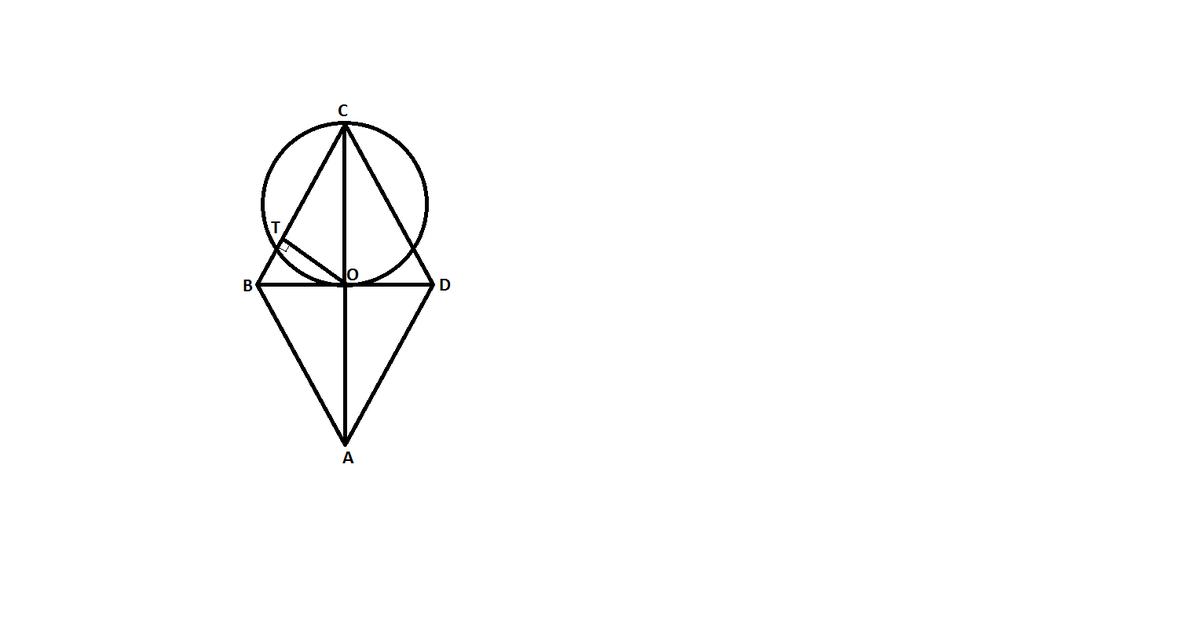

Ответы
Автор ответа:
1
Находим половину диагонали ВО = √((√3)²+3²) = √(3+9) = √12 =2√3.
Из подобия треугольников ОВТ и ОВС записываем пропорцию:
ВТ / ОТ = ВО / ОС.
Отсюда находим ОС = ОТ*ВО / ВТ = 3*2√3 / √3 = 6.
Радиус окружности равен половине ОС =6 / 2 = 3.
Теперь рассмотрим треугольник СО₁Т, где О₁ - центр окружности.
Сторона ВС = √(ВО²+ОС²) = √(12+36) = √48 = 4√3.
Сторона СТ = ВС - ВТ = 4√3 - √3 = 3√3.
Площадь искомого сегмента равна площади сектора с радиусами О₁т и О₁С. Угол между ними 120° (находится по теореме косинусов)
Высота треугольника равна половине радиуса.
Тогда S = (πR²α / 360) - ((1/2)(3/2)(3√3)) = (12π-9√3) / 4 = 5.52766 кв.ед.
Из подобия треугольников ОВТ и ОВС записываем пропорцию:
ВТ / ОТ = ВО / ОС.
Отсюда находим ОС = ОТ*ВО / ВТ = 3*2√3 / √3 = 6.
Радиус окружности равен половине ОС =6 / 2 = 3.
Теперь рассмотрим треугольник СО₁Т, где О₁ - центр окружности.
Сторона ВС = √(ВО²+ОС²) = √(12+36) = √48 = 4√3.
Сторона СТ = ВС - ВТ = 4√3 - √3 = 3√3.
Площадь искомого сегмента равна площади сектора с радиусами О₁т и О₁С. Угол между ними 120° (находится по теореме косинусов)
Высота треугольника равна половине радиуса.
Тогда S = (πR²α / 360) - ((1/2)(3/2)(3√3)) = (12π-9√3) / 4 = 5.52766 кв.ед.
Приложения:
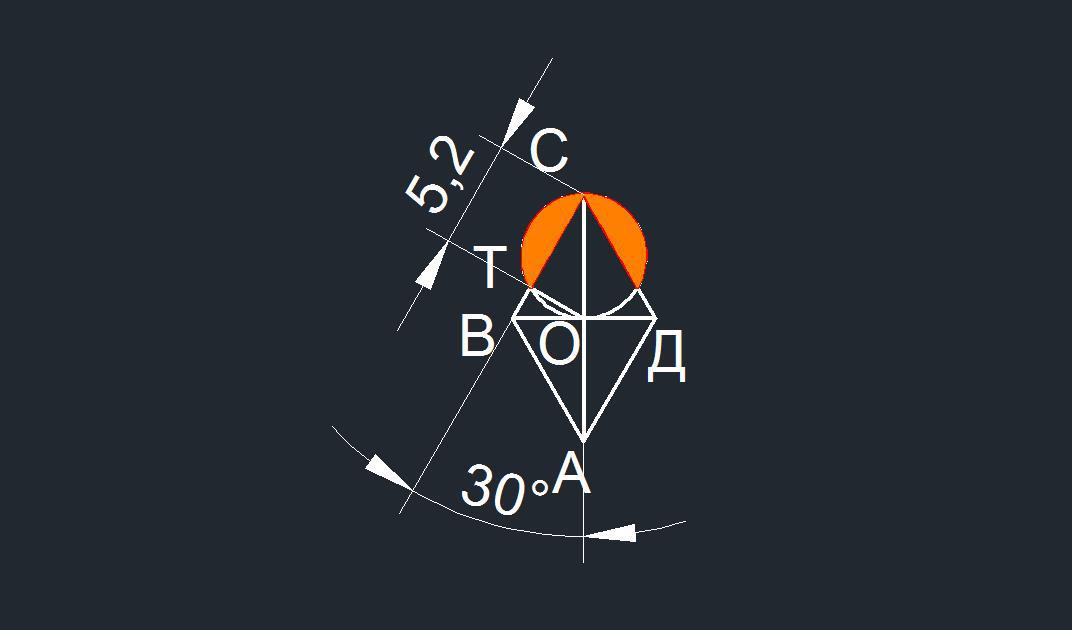
rysvlad:
а там сумма площадей сегментов? и не могли бы вы расписать в ворде где более понятны вычисления, а то нахождение площади немного непонятно мне
Похожие вопросы
Предмет: Другие предметы,
автор: NiceJora
Предмет: Окружающий мир,
автор: Matematik1211212
Предмет: Другие предметы,
автор: Аноним
Предмет: Химия,
автор: arina1658
Предмет: Английский язык,
автор: alinakorobova