Помогите! срочно.
Найдите площадь равнобедренной трапеции, если её основания равны 5 см и 17 см, а боковая сторона равна 10 см.!!! помогите
Ответы
HM=BC=5см
AH+MD=AD-BC=17-5=12см
AH=MD=12:2=6см
По теореме Пифагора
BH*=AB*-AH*=10*-6*=100-36=64
BH=квадратный корень из 64=8
S=одна вторая(BC+AD)xBH=одна вторая(5+17)x8=88см*
*- в квадрадрате
Ответ:
88 см²
Объяснение:
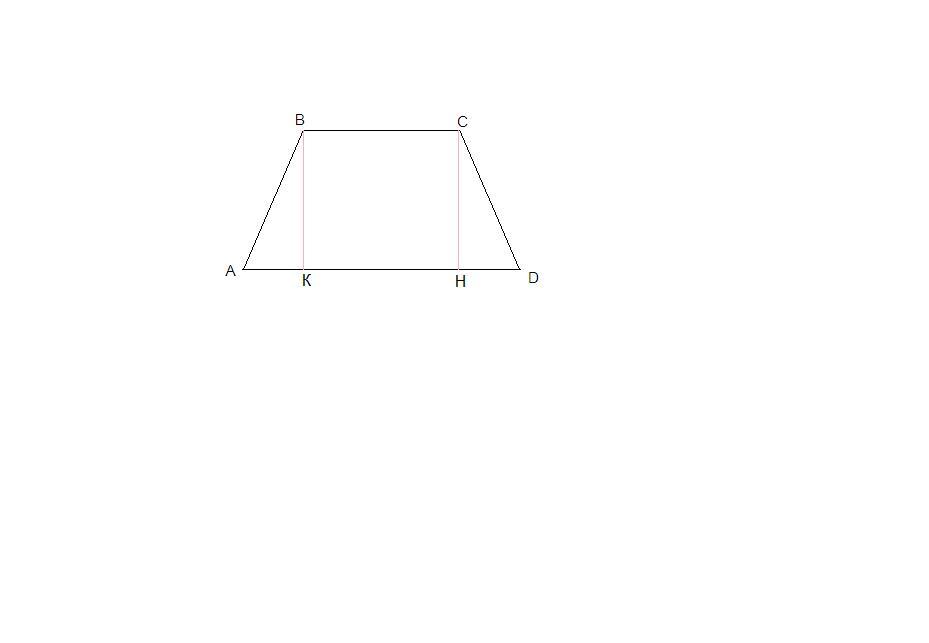
ВС = 5 см, AD = 17 см, АВ = CD = 10 см.
Проведем высоты ВК и СН.
ВК║СН как перпендикуляры к одной прямой, ВС║КН, ⇒
ВКНС - прямоугольник,
КН = ВС = 5 см
ΔАВК = ΔDCH по гипотенузе и катету:
∠АКВ = ∠CHD = 90°,
АВ = CD по условию,
ВК = СН как высоты трапеции,
значит АК = НD = (AD - КН)/2 = (17 - 5)/2 = 6 см
ΔАКВ: ∠АКВ = 90°, по теореме Пифагора:
ВК = √(АВ² - АК²) = √(10² - 6²) = √(100 - 36) = √64 = 8 см
Sabcd = 1/2 (AD + BC) · BK
Sabcd = 1/2 (17 + 5) · 8 = 1/2 · 22 · 8 = 88 см²