Предмет: Алгебра, автор: ebri

Решите пожалуйста очень нужно

Приложения:

Ответы

Автор ответа: agelena
0
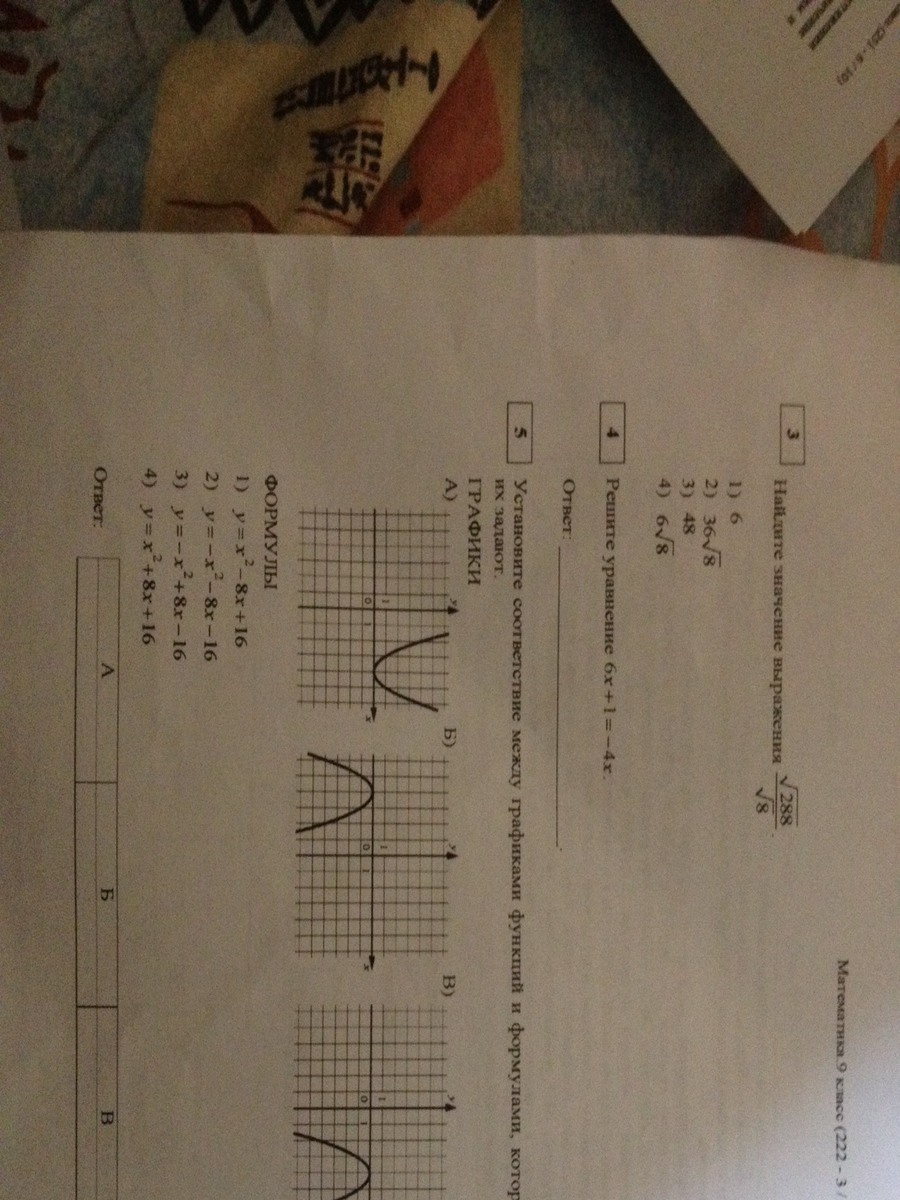
3.1)6
4.6x+1=-4x
6x+4x+1=0
10x=-1
x=-(1÷10)
Предыдущий вопрос
Следующий вопрос
Похожие вопросы
Предмет: Английский язык, автор: Принцесска10000
Притяжательные местоимения (The Possessive Pronouns)
Вставьте притяжательные местоимения там, где это необходимо.
Is that Mark's trumpet? Yes, it's his. It's his trumpet.(ОБРАЗЕЦ)
1. Is that Jessica's computer? — No, it isn't …. It's … … .
2. Is that Jason's motorbike? — Yes, it's …. It's … … .
3. Is that Bill and Laura's TV? — No. it isn’t …. It's … … .
4. Is that John's telephone? — No, it isn't …. it's … … .
5. Are those Mike's balloons? — Yes, they're …. They're … … balloons.
6. Is that Denise’s car? — No, it isn't …. It's … … .
7. Is that Andrew and Lucy's house? — Yes. it's …. It's … … house.
8. Are those my books? — No, they're not … .They're … … .
2 года назад
Предмет: Русский язык, автор: kirill1s
из 12,13 главок поэмы "Мцыри" выписать деепричастия вместе с глаголами, к которым они относятся
2 года назад
Предмет: Русский язык, автор: Prostakfsg
Пожалуйста помогите))) Заранее Спасибо !!! Вставьте знаки препинания, подчеркните главные члены предложения и обстоятельства образа действия.
Где-то двлеко за небосклоном словно про себя ворчал гром сердито и глухо..Мы обязаны бережно хранить памятники как немых свидетелей легендарного прошлого . Мне было хорошо как рыбе в воде. Как пахарь битва отдыхает. Луна как бледное пятно сквозь тучи мрачные желтела. Слова то шелестят как трава, то бормочут как родники, то пересвистываются как птицы, то позванивают как лед. Словно разъяренный зверь река металась в своих берегах. Душный воздух неподвижен как вода лесного озера.
2 года назад
Предмет: Литература, автор: Nelogi4niy
Какую первую фразу произнёс маленький принц при своём появлении?
"Маленький принц"
Пожалуйста.
8 лет назад
Предмет: Русский язык, автор: ematinaalisa
Помогите с русским
ворота тяжело закачались, раздался ужасающий скрип и треск, и левая воротина медленно отворилась. разбор 4
(повест., невоскл., грам.основа-
8 лет назад