Предмет: Математика,
автор: Alexvvv19
вычислите методом замены переменной
Приложения:
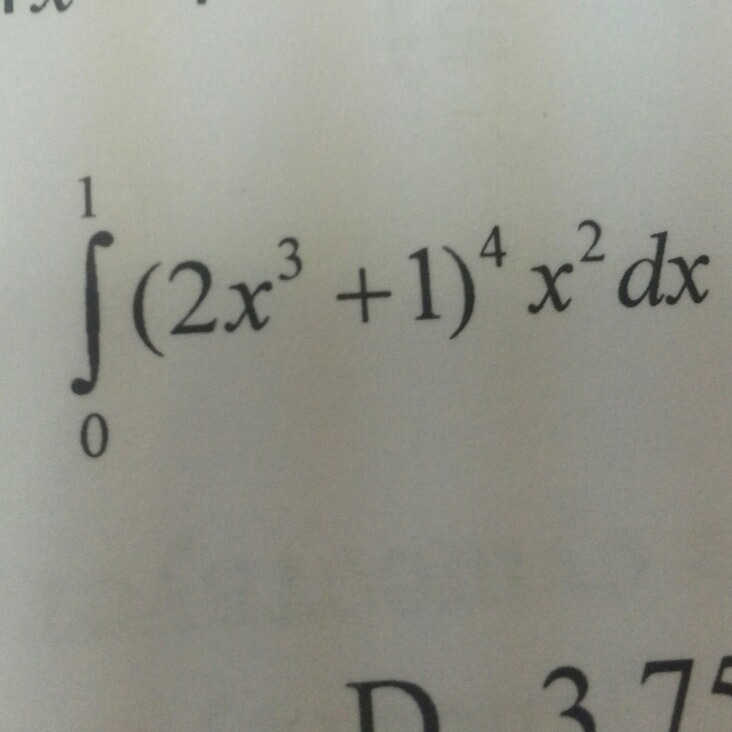
Ответы
Автор ответа:
0
(2x^3+1)^4*x^2dx
(2x^3+1)^4*1/2*1/3*d(2x^3+1)
1/6(2x^3+1)*d(2x^3+1)
Проведем замену переменной z=2x^3+1
при этом изменятся пределы интегрирования
x=0 z=2*0+1=1
x=1 z=2*1+1=3
Берем интеграл 1/6Szdz=1/6*1/2*z^2=1/12 z^2 в пределах от 1 до 3.
1/12[3^2-1^2]=8/12=2/3
(2x^3+1)^4*1/2*1/3*d(2x^3+1)
1/6(2x^3+1)*d(2x^3+1)
Проведем замену переменной z=2x^3+1
при этом изменятся пределы интегрирования
x=0 z=2*0+1=1
x=1 z=2*1+1=3
Берем интеграл 1/6Szdz=1/6*1/2*z^2=1/12 z^2 в пределах от 1 до 3.
1/12[3^2-1^2]=8/12=2/3
Похожие вопросы
Предмет: Русский язык,
автор: alina0901200432
Предмет: Қазақ тiлi,
автор: xeniyaforevermailru
Предмет: Русский язык,
автор: вдымфоо
Предмет: Химия,
автор: tyty12351
Предмет: Алгебра,
автор: GgTom67