Предмет: Геометрия, автор: maxmaxr

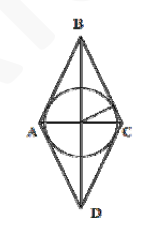
Найдите площадь ромба АВСD, если известно, что диагональ АС
равна 4, а радиус вписанной в него окружности равен 4/корень из 5

Приложения:

Gladiator359: Либо опечатка, либо исправь дано. АС не может быть меньше радиуса.

maxmaxr: В условии все именно так. И АС не меньше радиуса )

Gladiator359: У вас в дано записано, что АС=4, а радиус 4корня из 5, что примерно равно 9. тогда радиус больше АС, что невозможно.

Gladiator359: Дано исправите, решу за 3 минуты.

maxmaxr: 4 деленное на корень из 5

Ответы

Автор ответа: Gladiator359

Пусть О- центр окружности, ОЕ- r; r перпендикулярен к касательной окружности. Тогда △BOC~△OEC, т.к ∠OEC=∠BOC=90 и ∠BCO- общий(по 2 углам).
По теореме Пифагора:
$EC= \sqrt{ 4-\frac{16}{5} }= \sqrt{ \frac{20-16}{5}}= \frac{2}{ \sqrt{5} }$
=> $\frac{OC}{BO}= \frac{EC}{OE}$
$\frac{2}{BO}= \frac{2}{ \sqrt{5} }: \frac{4}{ \sqrt{5} } = \frac{2}{ \sqrt{5} } \frac{ \sqrt{5} }{4}$
=0,5; BO=2: 0,5=4 =>BD=8
А т.к AC=4, то $S_{romb}= \frac{ d_{1} d_{2} }{2} = \frac{8*4}{2} =16cm^{2}$