Предмет: Алгебра,
автор: nika15s150798
Help!С подробным решением,пожалуйста.
Приложения:

Ответы
Автор ответа:
1
6 решил, остальное как решать не ведаю.
Приложения:

Автор ответа:
1
Здесь проведём оценку числителя. Косинус лежит в отрезке [-1;1]. То есть в этом отрезке лежит дробь (3-√13)/2. Домножим на 2 края отрезка и саму дробь, чтобы избавиться от знаменателя. Получим, что 3-√13 должна лежать в отрезке [-2;2]. Очевидно, что 3<√13, поскольку их квадраты оцениваются так же (9<13), то есть 3-√13<0. То есть 3-√13 гарантировано <2. Нужно показать, что 3-√13>=-2. Для этого перенесём -2 в левую часть, а корень - в правую.
3+2>=√13
5>=√13
Возведём в квадрат
25>=13 - верно, значит 3-√13>=-2. Мы предположили это и пришли к верному выводу, значит наше предположение верно. То есть нас устраивает только один из корней - (3-√13)/2
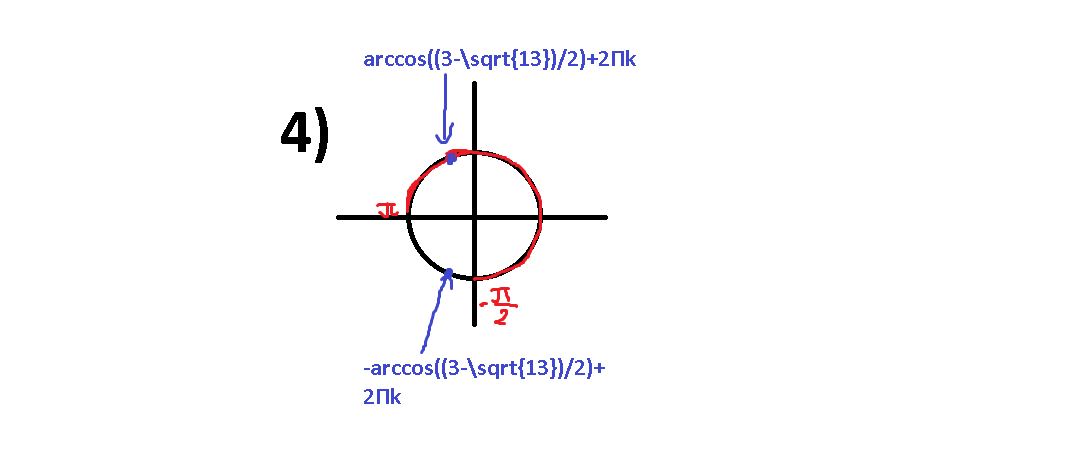
Дальше будет проще воспользоваться единичной окружностью: изобразим этот интервал и посмотрим, какие точки туда попадают. Исходя из рисунка очевидно, что для положительного решения нужно взять k=0, то есть
Дальше можно решить двумя путями: через неравенства или же аналогично предыдущему примеру через окружности. Я просто напишу, какие корни попадают, чтобы решение не показалось слишком большим.
sin²x=5/4 решений не имеет, так как, если опустить корень, то полученное число - √5 /2 - больше единицы, а синус лежит в отрезке [-1;1].
У второго уравнения решений нет, так как слева стоит квадрат, который неотрицателен для любого x, а справа - отрицательное число.
Объединим в одно решение:
Приложения:
Hunter996:
В шестом, вроде как, не хватает решения 3П/4 + Пк, и тогда ещё одно решение добавится - 3П/4
Шестое неверно. Сейчас исправлю
Поправил
Я немного не поняла 7 задание,каким образом там появился тангенс?
Формула,поняла)
Похожие вопросы
Предмет: Другие предметы,
автор: 1945264
Предмет: Русский язык,
автор: alina0901200432
Предмет: Русский язык,
автор: tuguhol
Предмет: Геометрия,
автор: samat3400
Предмет: Математика,
автор: VatikanikLusik33