Предмет: Математика,
автор: vanilka666
ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
Приложения:
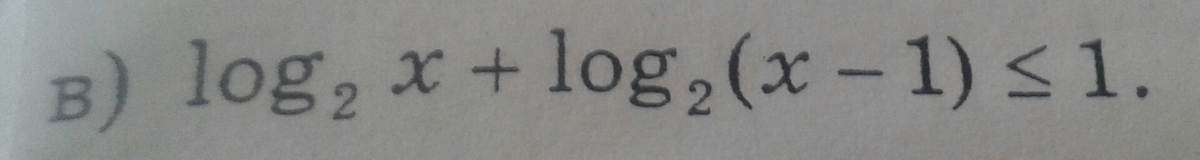
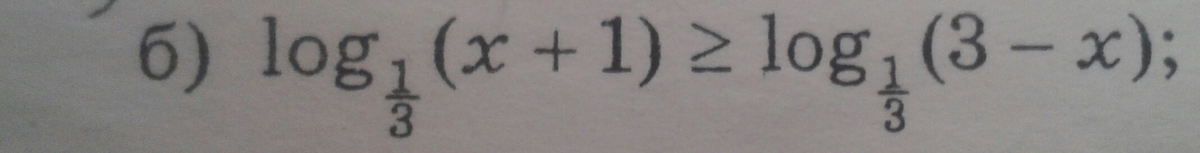
Ответы
Автор ответа:
0
б) log(₁/₃) (x+1)≥log(₁/₃)(3-x) ,ОДЗ х+1>0 x> -1 , 3-x>0 x<3
так как основание логарифмов меньше единицы (1/3<1) , значит знак неравенства меняем:
х+1≥3-х
х+х≥3-1
2х≥2
х≥1
x∈(-1; 1}
в) log₂ x + log₂ (x-1) ≤ 1 ОДЗ х>1
log₂(x·(x-1)) ≤ log₂ 2
основание логарифма больше единицы, поэтому знак неравенства не меняем
х(х-1)≤2
х²-х-2≤0 х²-х-2=0 D=9 x1=(1-3)\2= -1 x2=(1+3)\2=2
+ - +
_________ -1__________2__________
с учетом ОДЗ х∈ (1 ;2]
Похожие вопросы
Предмет: Английский язык,
автор: kamola555
Предмет: Английский язык,
автор: РыбкаНемо1
Предмет: Русский язык,
автор: irinkashevozt722
Предмет: Русский язык,
автор: OLYAJSJSJS