Question

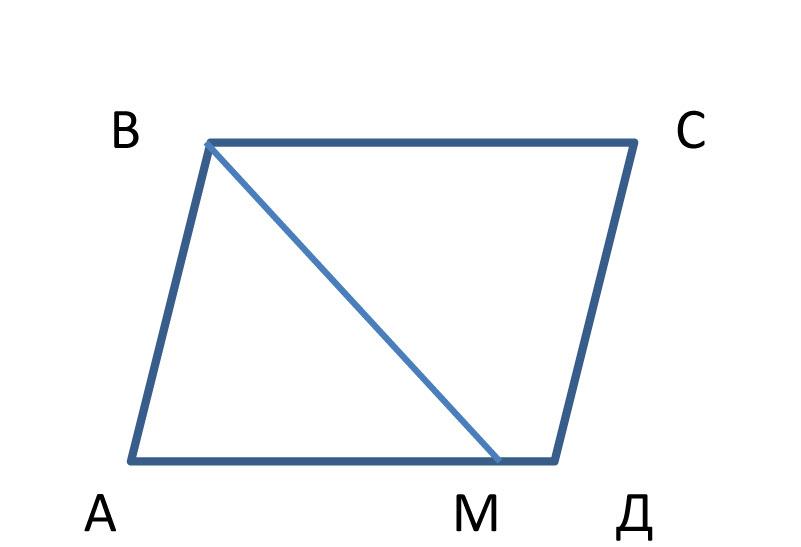
В параллелограмме ABCD биссектриса угла В пересекает сторону AD в точке М так, что AM в 4 раза больше MD.
Найдите длины сторон параллелограмма, если его периметр 36 см.
Рисунок обязателен.

Answer 1

Биссектриса ВМ угла параллелограмма АВСД отсекает от него равнобедренный треугольник АВМ (АВ=АМ).
По условию АМ=4МД или МД=АМ/4
Значит АД= АМ+МД=АМ+АМ/4=5АМ/4
Периметр параллелограмма Р=2(АВ+АД)=2(АМ+5АМ/4)=9АМ/2=4,5АМ
АМ=Р/4,5=36/4,5=8 см
Тогда стороны АВ=СД=8см
АД=ВС=5*8/4=10 см
Ответ 8см, 10см, 8см, 10см