Предмет: Геометрия,
автор: Realmadrid2000
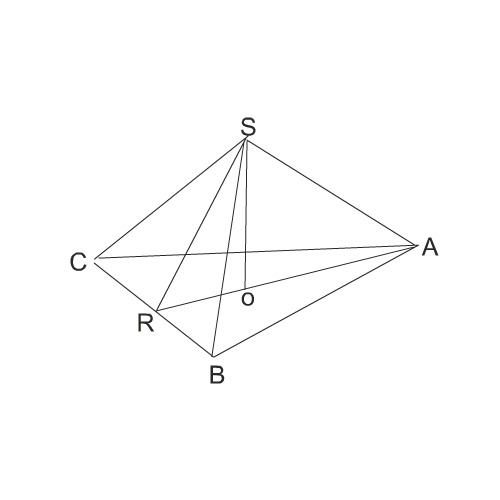
в правильной пирамиде SABC R- середина ребра BC, S-вершина. Известно что AB=8, а площадь боковой поверхности равна 252. Найдите длину отрезка SR
Ответы
Автор ответа:
0
SR - апофема пирамиды. Площадь боковой поверхности состоит из суммы площадей 3-х равных треугольников, которые являются боковыми гранями пирамиды. То есть . В данном случае речь идет о треугольнике BSC. так как площади треугольников равны, то можно записать в следующем виде
Делим обе части на 3.
. Так как треугольник BSR - равнобедренный (из того, что пирамида -правильная), то его площадь равна произведению половины основания BC на высоту SR. Так как пирамида правильная, то AB=BC.
. Делим обе части уравнения на 4.
, то есть SR=21.
Автор ответа:
0
В правильной пирамиде все грани равны.
Площадь одной грани
Sграни=SR·CR
Sграни=Sбок:3
Стороны АВС равны.
Sграни=SR·CR
CR=AB:2=8:2=4
S бок=SR·CR·3
SR=S бок:(3·CR)
252=SR·4·3
SR=252:12
SR=21
Приложения:
Похожие вопросы
Предмет: Физика,
автор: anyashchurko2006
Предмет: Українська мова,
автор: enaung
Предмет: Литература,
автор: sitdikovradomir8
Предмет: Математика,
автор: Linka28
Предмет: География,
автор: evgenyaa