Question

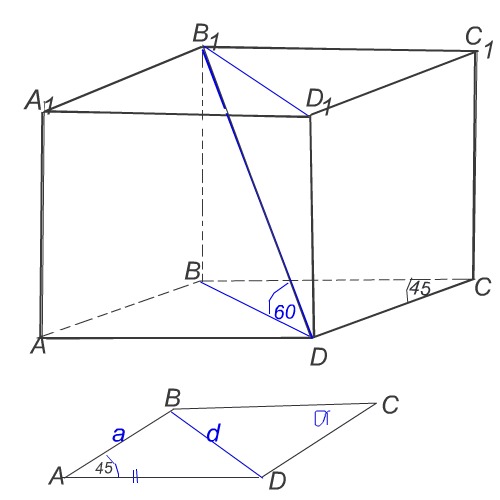
сторони основ прямокутного паралелепіпеда = 12 см та 12√2 см і утворюють кут 45 градусів, а менша діагональ паралелепіпеда- кут 60 градусів з площиною основи. Знайдіть площу меншого діагонального перерізу.

Answer 1

Площадь меньшего диагонального сечения  параллелепипеда равна произведению его высоты BB₁ на основание ВD .

Основание BD=диагональ BD параллелограмма АВСD.

Формула диагонали через стороны и углы параллелограмма (по теореме косинусов) (D, d)
d²=а² + b² - 2ab·cosα

d²=144+288 - 2·12·12√2 ·cos(45°)
d²=144+288 - 288 √2 ·(√2):2)
d =√ 144=12

BD=12 см

Высота BB1:ВD=tg (60°) = tg (π/3) = √3
BB₁=12·√3=12√3

S DBB₁D₁=ВD·BB₁=12·12√3=144√3 см²