Предмет: Геометрия, автор: Аноним

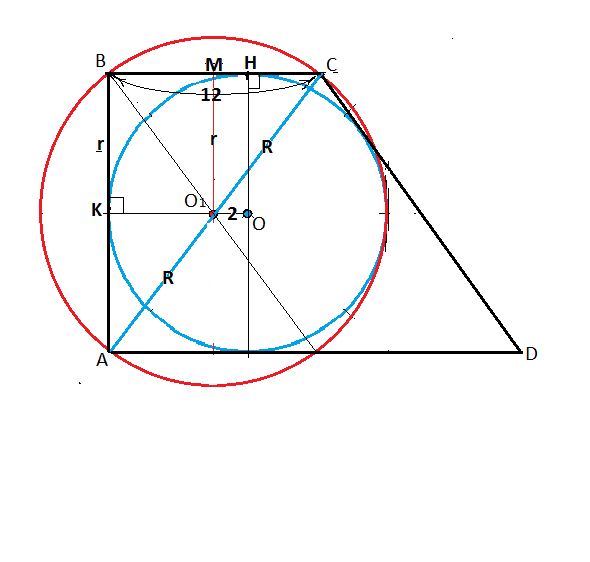
В прямоугольную трапецию АВСD(AB┴ВС,АВ┴АD) вписана окружность с центром в точке О. Через точки А,В,С проведена окружность с центром в точке О1. Найдите диагональ АС, если ОО1=2 см, а меньшее основание ВС=12см. НУЖЕН ЧЕРТЕЖ

Ответы

Автор ответа: oganesbagoyan

AC² =AB² +BC² ;
AC² =(2r)² +BC² ;
===============
OO₁= r -BC/2 .
2 =r - 12/2;
r =8 ;
AC² =(2*8)² +12² =( 4*4)² +(4*3)² =4²(4²+3²) =4²*5² ;
AC =4*5 =20.

Аноним: Мне нужен рисунок

Аноним: Очень

oganesbagoyan: ABC прямоугольный треугольник можно построить по катетам BC =4*3 и AB =4*4 ; O₁_середина гипотенузы AC . Провести окружность вписанной в ABCD радиусом r =4 AD || BC (параллельно )

oganesbagoyan: Из точки B [ одна из вершин (условно 3 -ая) ] провести касательную к этой окружности . Точка пересечения касательной и линии a проведенной из A паралл . a|| BC определяет вершину D . Все элементарно .

Аноним: А где o1 находится

oganesbagoyan: Я уже написал O₁_середина гипотенузы AC .

Аноним: Ясно, спасибо

Автор ответа: Hrisula

Центр О1 описанной окружности треугольника АВС лежит на пересечении срединного перпендикуляра катета ВA и гипотенузы АС, т.е. центры обеих окружностей лежат на средней линии трапеции и ОО1=2 см.
Пусть радиус описанной окружности треугольника АВС будет R, точка касания вписанной окружности
на ВC-Н,
на АВ-К.
радиус вписанной в трапецию окружности r.
r=KO+OO1
КО- средняя линия треугольника АВС
КО= ВС:2=12:2=6 см
r=6+2=8 см
ВМ=высота и медиана равнобедренного прямоугольника ВО1С
В прямоугольном треугольнике ВМО1 катет
МО1=НО=r=8 см
катет ВМ=6 см, отношение катетов 3:4,⇒
ВО1=10 как гипотенуза египетского треугольника ( можно проверить т. Пифагора)
АС=2R=2*10=20 см

Приложения: