Предмет: Алгебра,
автор: Moroshenka
Помогите дорешать определенный интеграл, препод начало решения проверила сказала что всё правильно... а как дальше?
если плохо видно, то верхний предел  , а нижний
, а нижний  .
.
Желательно решение подробненько расписать)
Приложения:
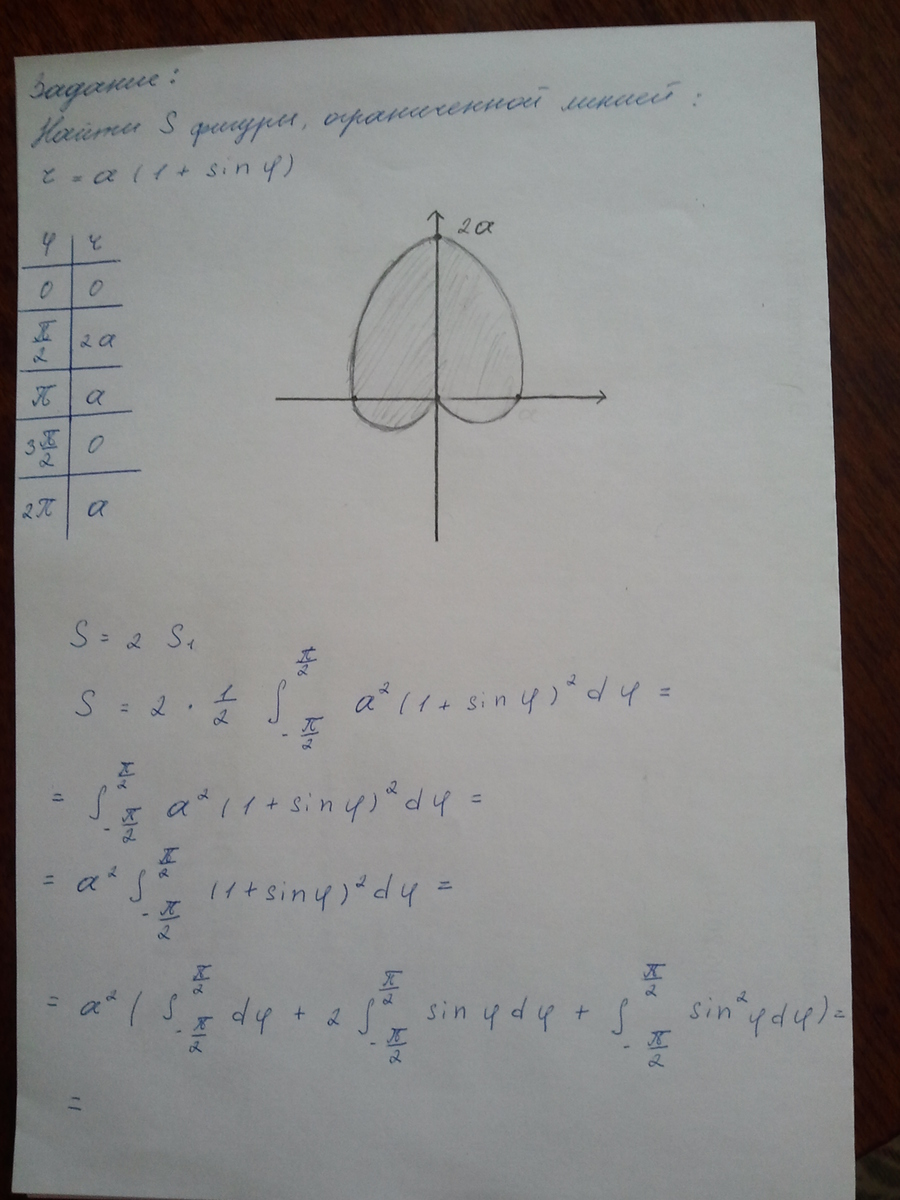
Ответы
Автор ответа:
1
Moroshenka:
Спасибо большое!)
Я тебя обожаю!
Похожие вопросы
Предмет: Русский язык,
автор: vovan0404
Предмет: Русский язык,
автор: nicorozenberg
Предмет: Русский язык,
автор: Bazzigamer
Предмет: Математика,
автор: am0783657
Предмет: Физика,
автор: den4ikcool