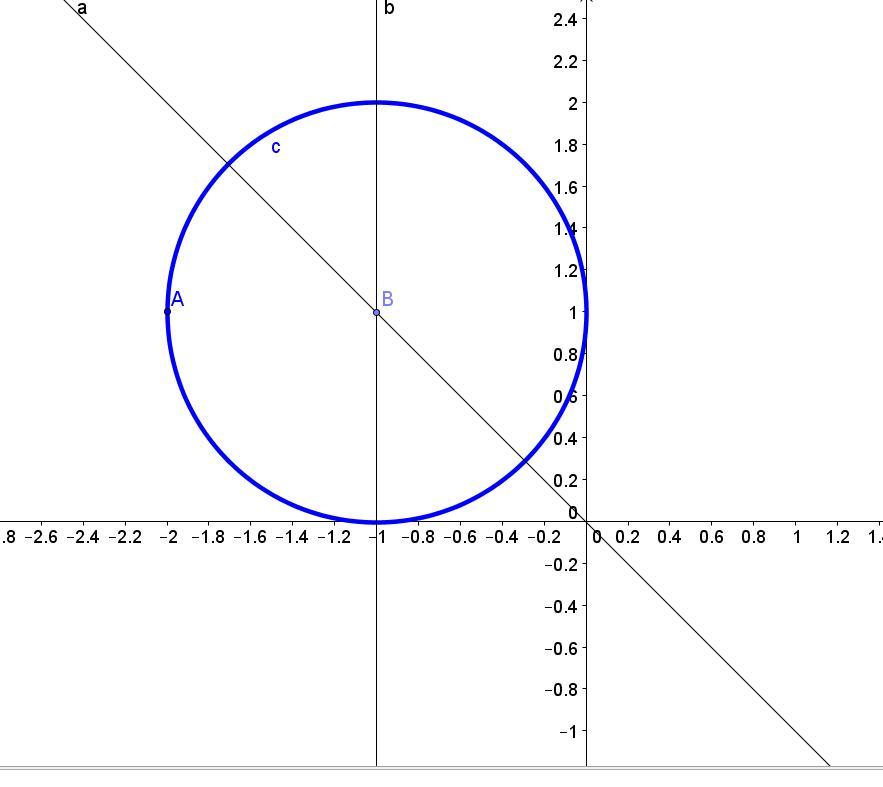
найдите центр и радиус окружности, касающейся осей координат и проходящей через точку А( -2;1)
Ответы
Найдите центр и радиус окружности, касающейся осей координат и проходящей через точку А( -2;1).
Если окружность касается осей координат и проходит через точку А( -2;1). то эта окружность расположена во второй четверти.
Её центр находится на биссектрисе прямого угла, уравнение которой у = -х. Примем координаты центра B(xB; yB) или с учётом у = -х: B(xB; -хB).
Уравнение окружности с учётом точки А: (-2 - хВ)² + (1 + хВ)² = R².
4 + 4xB + хВ² + 1 + 2xB + хВ² = R².
Но по условию касания осей R = -xB (точка В отстоит от оси координат на величину радиуса) или R² = хВ².
4 + 4xB + хВ² + 1 + 2xB + хВ² = xB².
Получаем квадратное уравнение:
хВ² + 6xB + 5 = 0.
Дискриминант D = 36 – 4*1*5 = 16, √D = 4.
хВ1 =(-6 – 4)/2 = - 5 .
хВ2 =(-6 + 4)/2 = - 1 .
Получили два решения задачи.
Ответ: центр (-5; 5), R = 5.
центр (-1; 1), R = 1.
К решению даётся один рисунок для второго случая.