Question

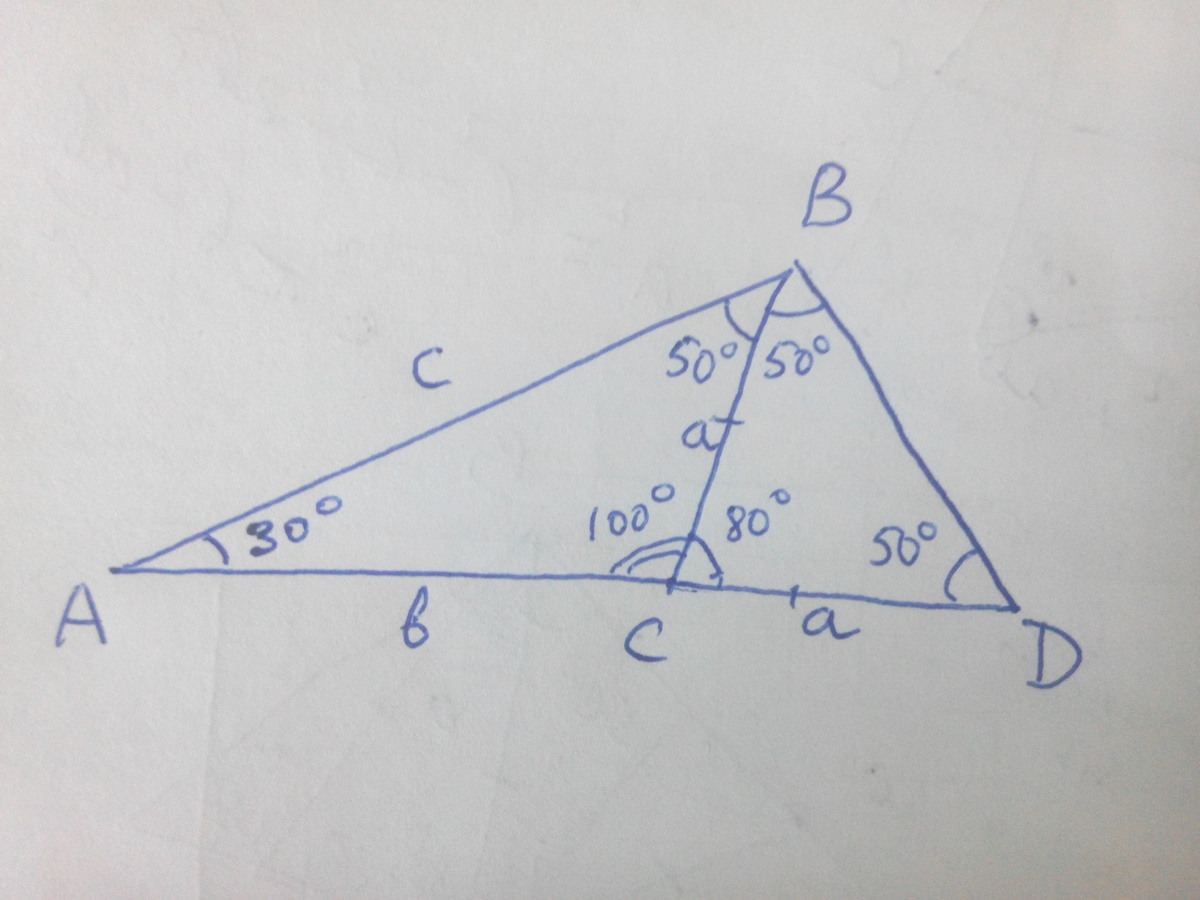
В треугольнике АВС угол А равен 30 градусов, а угол В равен 50 градусам.
Доказать, что стороны треугольника связаны соотношением c^2=b(a+b).
Решение точно не через теорему синусов.
Рисунок обязателен.

Answer 1

Пусть BC=a, AC=b, AB=c. На продолжении стороны AC за точку C возьмем точку D так, что CD=CB=a, Тогда AD=a+b и
∠CDB=(180°-∠BCD)/2=(180°-80°)/2=50°=∠ABC.
Значит треугольники ABC и ADB подобны по двум углам. Отсюда AD/AB=AB/AC, т.е. (a+b)/c=c/b, что и требовалось.