Предмет: Геометрия,
автор: natalyalarikova
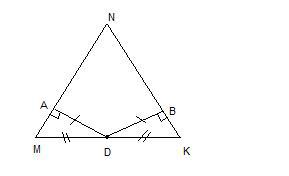
В остроугольном треугольнике MNK из точки D, середины стороны MK, проведены перпендикуляры DA и DB к сторонам MN и NK, докажите, что если DA=DB, то треугольник MNK равнобедренный
Ответы
Автор ответа:
38
Рассмотрим прямоугольные треугольники MAD и KBD. Они равны по одному из признаков равенства прямоугольных треуг-ов: гипотенуза и катет одного треуг-ка соответственно равны гипотенузе и катету другого:
- гипотенузы DM и DK равны по условию;
- катеты DA и DB равны по условию также.
У равных треугольников равны и соответственные углы М и К. Значит, треугольник MNK равнобедренный, т.к. углы при его основании МК равны между собой.
- гипотенузы DM и DK равны по условию;
- катеты DA и DB равны по условию также.
У равных треугольников равны и соответственные углы М и К. Значит, треугольник MNK равнобедренный, т.к. углы при его основании МК равны между собой.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Nurdaulet20041
Предмет: Окружающий мир,
автор: АлесяПо1
Предмет: Русский язык,
автор: Амеля11
Предмет: Физика,
автор: maksim2015vip
Предмет: Химия,
автор: mary004009004