Предмет: Геометрия,
автор: nelton
В треугольнике АВС биссектриса ВЕ и медиана АD перпендикулярны и имеют одинаковую длину, равную 92.Найти стороны этого треугольника.
Ответы
Автор ответа:
0
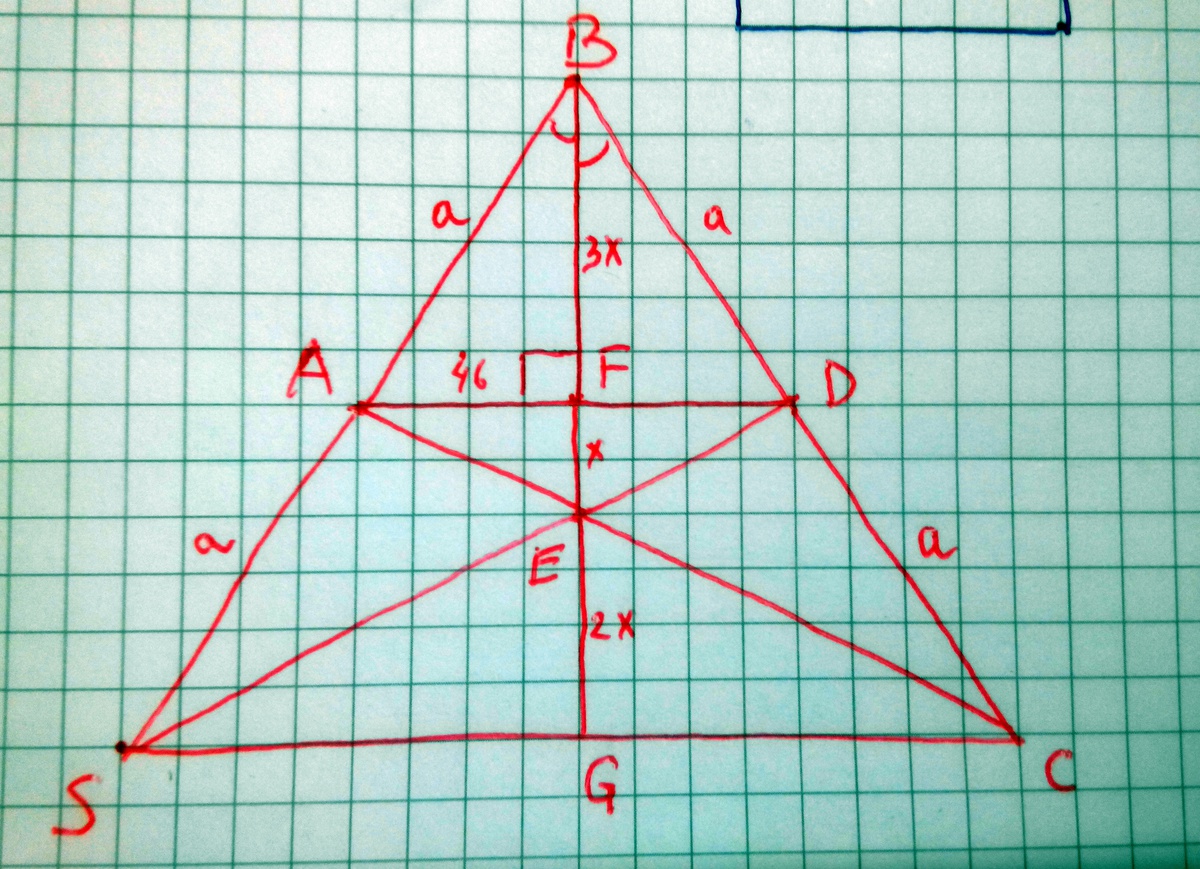
Пусть AD пересекает BE в точке F. ABD - равнобедренный (т.к. BF его биссектриса и высота), т.е. AB=BD=DC=a. На продолжении прямой BA за точку A возьмем точку S, так что AB=AS, т.е. SBC - равнобедренный треугольник и BS=BC=2a. AD - его средняя линия. Пусть BG - высота треугольника SBC. Пусть FE=x. Т.к. SC=2AD, то EG=2x, значит BF=FG=3x. Отсюда BE=BF+FE=3x+x=4x=92, т.е. x=23. Т.к. AF=92/2=46, то по т. Пифагора для треугольника AFE получим  . По свойству биссектрисы BE получаем EC=2AE и, следовательно,
. По свойству биссектрисы BE получаем EC=2AE и, следовательно,  .
.
По т. Пифагора для треугольника ABF получим .
. .
.
По т. Пифагора для треугольника ABF получим
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: лера1550
Предмет: Английский язык,
автор: dogfeya27
Предмет: Английский язык,
автор: Novoless
Предмет: Математика,
автор: Recrut00
Предмет: Литература,
автор: Аноним