Предмет: Геометрия,
автор: Миньон69
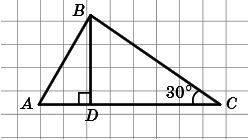
Отрезок BD— высота треугольника ABC, изображенного на рисунке, CD = 9 см, AD = 3 см. Какова длина стороны AB?
Приложения:
Ответы
Автор ответа:
9
Треугольник АВD - прямоугольный.
АВ можно найти по т. Пифагора:
АВ²=АD²+BD²
BD (если уже знаете тангенс)
BD:DC=tg (30°)=1/√3
BD=DC*tg(30°)=3√3
BD²=27
AB²=9+27=36
AB=√36=6 см
--------------
Если пока еще не знакомы с функциями углов, в решении можно пользоваться т.Пифагора.
Из прямоугольного треугольника ВDС ВС=2BD
( BD противолежит углу 30° и потому ВС=2 BD
BD²=(2BD)²-CD³
BD²=4BD²-81
-3BD²= -81
BD²=27
----дальнейшее решение то же самое, что в предыдущем варианте.
Ответ:АВ=6 см
--
bzs@
АВ можно найти по т. Пифагора:
АВ²=АD²+BD²
BD (если уже знаете тангенс)
BD:DC=tg (30°)=1/√3
BD=DC*tg(30°)=3√3
BD²=27
AB²=9+27=36
AB=√36=6 см
--------------
Если пока еще не знакомы с функциями углов, в решении можно пользоваться т.Пифагора.
Из прямоугольного треугольника ВDС ВС=2BD
( BD противолежит углу 30° и потому ВС=2 BD
BD²=(2BD)²-CD³
BD²=4BD²-81
-3BD²= -81
BD²=27
----дальнейшее решение то же самое, что в предыдущем варианте.
Ответ:АВ=6 см
--
bzs@
Похожие вопросы
Предмет: Окружающий мир,
автор: kec9637
Предмет: Русский язык,
автор: youtuber5
Предмет: Русский язык,
автор: НИНЗго
Предмет: Русский язык,
автор: glezdelena
Предмет: История,
автор: bedasofia14