Предмет: Алгебра,
автор: 4710
Найдите производнуюю плиииз
Приложения:
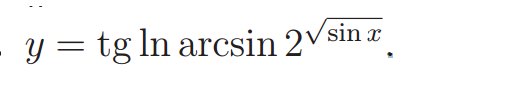
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: zoka1706
Предмет: Английский язык,
автор: JaikHit533
Предмет: Русский язык,
автор: 666228666
Предмет: Русский язык,
автор: polinawowv
Предмет: Информатика,
автор: Снежано4ка