Question

высота правильной треугольной пирамиды равна h, а двугранный угол при стороне основания равен 45 градусов. Найти площадь поверхности пирамиды

Answer 1

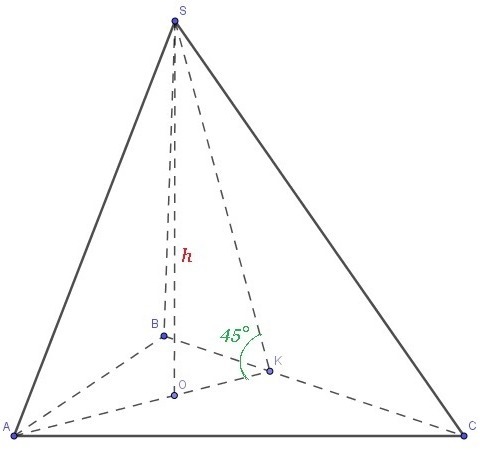
Рассмотрим прямоугольный треугольник $\tt SOK$, в нём $\tt \angle SKO=45а$, значит $\tt \angle OSK=90а-\angle SKO=90а-45а=45а$, следовательно, треугольник $\tt SOK$ - равнобедренный прямоугольный треугольник: $\tt SO=OK=h$

$\tt OK$- радиус вписанной окружности основания. Основанием правильной треугольной пирамиды является правильный треугольник $\tt ABC$

$\tt r=OK=\dfrac{AC}{2\sqrt{3}} ~~\Rightarrow~~ AC=2r\sqrt{3} =2h\sqrt{3}$

Площадь основания: $\tt S_{oc_H}=\dfrac{AC^2\sqrt{3}}{4}=\dfrac{(2h\sqrt{3})^2\cdot \sqrt{3}}{4}=3h^2\sqrt{3}$ кв. ед.

$\tt SK=\sqrt{SO^2+OK^2}=\sqrt{h^2+h^2}=h\sqrt{2}$ - апофема.

Площадь боковой поверхности:

$\tt S_{bok}=\dfrac{1}{2}\cdot P_{oc_H}\cdot SK= \dfrac{1}{2}\cdot 3\cdot2h\sqrt{3} \cdot h\sqrt{2} =3h^2\sqrt{6}$ кв.ед.

Площадь полной поверхности:

$\tt S=S_{oc_H}+S_{bok}=3h^2\sqrt{3}+3h^2\sqrt{6}=3h^2\sqrt{3}\left(1+\sqrt{2}\right)$ кв. ед.

Ответ: $\tt3h^2\sqrt{3}\left(1+\sqrt{2}\right)$ кв.ед..

Answer 2

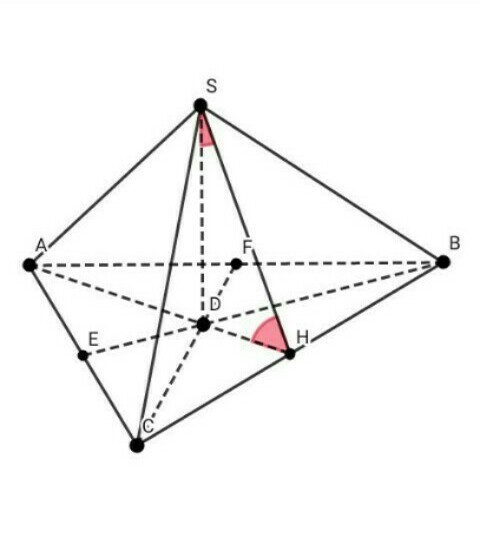
ДАНО: SАВС - правильная треугольная пирамида ; SD = h ; линейный угол двугранного угла ABCS равен 45°.

НАЙТИ: S пол. пов. пирамиды 
______________________________

РЕШЕНИЕ:

1) Линейным углом двугранного угла называется угол, образованный лучами с вершиной на ребре, и при этом лучи лежат на гранях двугранного угла и перпендикулярны ребру.

В основании правильной треугольной пирамиды лежит правильный треугольник, то есть ∆ АВС – равносторонний 

В ∆ АВС опустим высоту АН на ВС
В равностороннем треугольнике высота является и медианой, и биссектрисой → ВН = СН

отрезок SD ( высота пирамиды ) перпендикулярен плоскости основания ∆ АВС
Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости →
SD перпендикулярен АН
АН перпендикулярен ВС
Значит, SH перпендикулярен ВС по теореме о трёх перпендикулярах

Из этого следует, что угол SHА – линейный угол двугранного угла АВСS, то есть угол SHА = 45°

2) Рассмотрим ∆ SHD (угол SDH = 90°):
Сумма острых углов в прямоугольном треугольнике всегда равна 90°
угол HSD = 90° - 45° = 45°

Значит, ∆ SHD – прямоугольный и равнобедренный , SD = DH = h

По теореме Пифагора:
SH² = SD² + DH²
SH² = h² + h² = 2h²
SH = h√2

Как было сказано выше, высота, проведённая в равностороннем треугольнике, является и медианой, и биссектрисой
Медианы любого треугольника пересекаются в одной точке и точкой пересечения делятся в отношении 2 : 1 , считая от вершины
Следовательно, AD : DH = 2 : 1 →
AD = 2 × DH = 2h
AH = AD + DH = 2h + h = 3h

Сторона равностороннего треугольника вычисляется по формуле:

$a = \frac{2 \sqrt{3} h}{3}$

где а - сторона равностороннего треугольника, h - высота

BC = ( 2√3 × AH ) / 3 = ( 2√3 × 3h ) / 3 = 2√3h

S пол. пов. пирамиды = S осн. + S бок. пов.

В правильной треугольной пирамиде все боковые грани равны друг другу →

S пол. пов. пирамиды = S abc + 3 × S bcs 

Площадь равностороннего треугольника вычисляется по формуле:

$s = \frac{ {a}^{2} \sqrt{3} }{4}$

где а - сторона равностороннего треугольника

S пол. пов. пирамиды = 
$= \frac{ {(2 \sqrt{3}h) }^{2} \sqrt{3} }{4} + 3 \times \frac{1}{2} \times 2 \sqrt{3} h \times h \sqrt{2} = \\ = 3 \sqrt{3} {h}^{2} + 3 \sqrt{6} {h}^{2} = 3 \sqrt{3} {h}^{2} (1 + \sqrt{2} )$



ОТВЕТ: 3√3h² × ( 1 + √2 )