Предмет: Алгебра,
автор: netaliaburtcrva
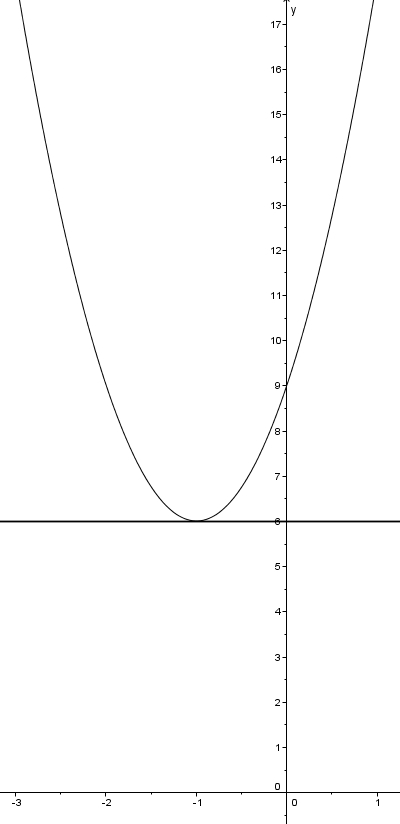
Исследовать на экстремум функцию y=x^3+3x^2+9x-6
Ответы
Автор ответа:
3
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Лампочка322
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Vladkrav
Предмет: Английский язык,
автор: ggsg2d
Предмет: Химия,
автор: aioychikiday