Question

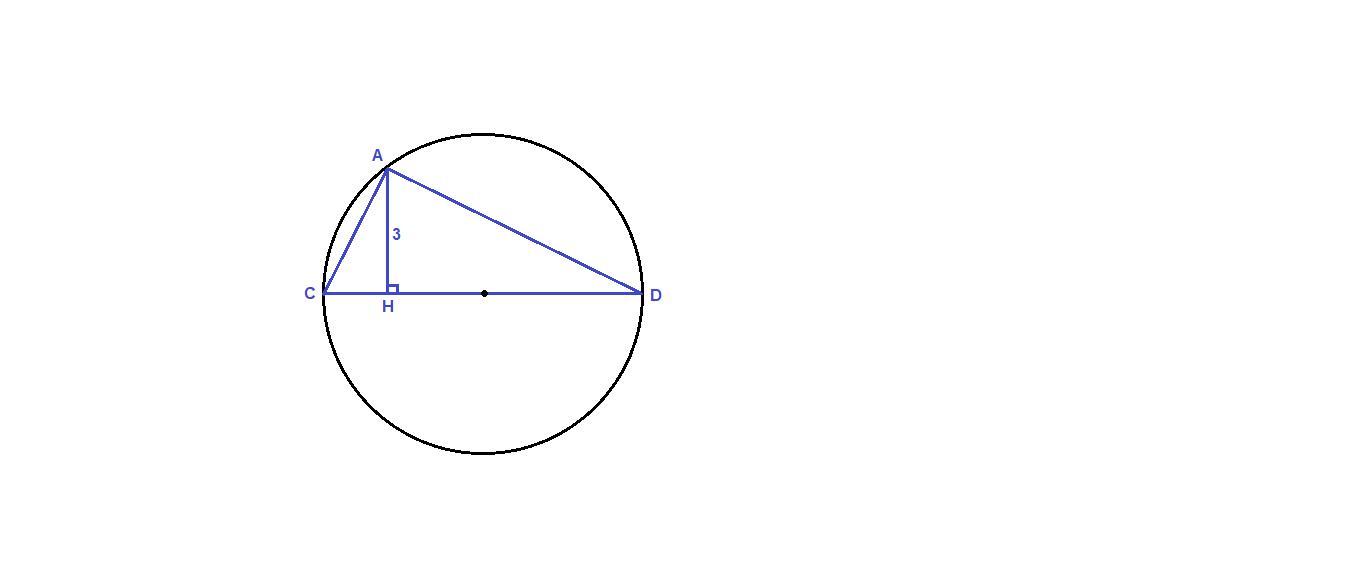
Отрезоз CD-диаметр окружности . отрезок AC-хорда этой окружности и AC: CD = 1:2 . Точка А удалена от прямой св на расстояние , равное 3 см . Вычислите ПЛОЩАДЬ треугольника ACD и длину радиуса окружности


ДАЮ 50 баллов!!!!!!!!!!!!!!!!

Answer 1

Неточность в вопросе: точка А удалена от прямой CD на расстояние, равное 3 см.

Ответ:

Sacd = 6√3 см²

R = 2√3 см

Объяснение:

∠DАС вписанный, опирается на полуокружность, значит

∠DАС = 90°.

АС - катет, равен половине гипотенузы, значит лежит против угла в 30°:

∠ADC = 30°.

ΔAHD: ∠АНD = 90°, ∠ADH = 30°, ⇒ AD = 2AH = 2 · 3 = 6 см

Обозначим радиус окружности R. Тогда CD = 2R, AC = CD/2 = R/

По теореме Пифагора из треугольника ACD:

AC² + AD² = CD²

R² + 36 = 4R²

3R² = 36

R² = 12

R = 2√3 см

AC = 2√3 см,

Sacd = 1/2 AC · AD = 1/2 · 2√3 · 6 = 6√3 см²