Предмет: Алгебра,
автор: Ювелинка
Тригонометрическое уравнение на фото.
Приложения:
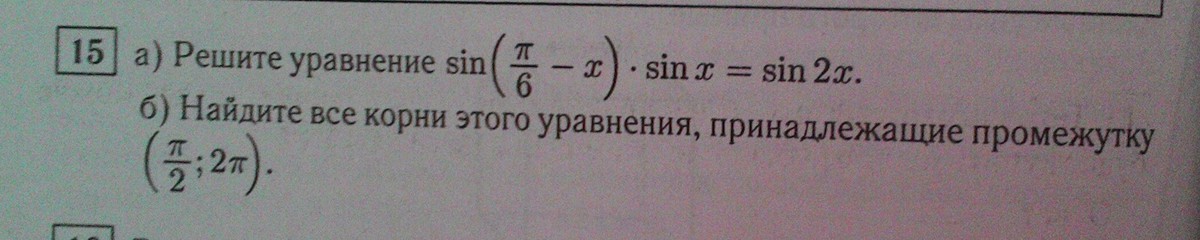
Ответы
Автор ответа:
0
Если sinx = 0, то x = 2πn, n∈Z
Если sinx ≠ 0, то делим обе части уравнения на sinx :
Ответ: 2πn U 2π/3 + πn, где n∈Z.
Задание б) На окружности отмечаем данный промежуток ( π/2 ; 2π ). На чертеже он отмечен красным цветом (концы не входят). Изображаем решения, которые попадают в этот промежуток, это только две точки -
2π - не входит в этот промежуток.
Ответ:
Приложения:
Ювелинка:
А можно подробнее под б) ?
Не тот файл загрузил случайно, вот ссылка на нужное изображение: https://yadi.sk/i/nzHzj-RUgCoGu
Похожие вопросы
Предмет: Английский язык,
автор: Aishusha05
Предмет: Другие предметы,
автор: mazoalexandra
Предмет: Русский язык,
автор: Adushkina07108
Предмет: Русский язык,
автор: boooooob
Предмет: Математика,
автор: weyima