Предмет: Математика,
автор: zamaraev1997
Найти два интеграла.....
Приложения:
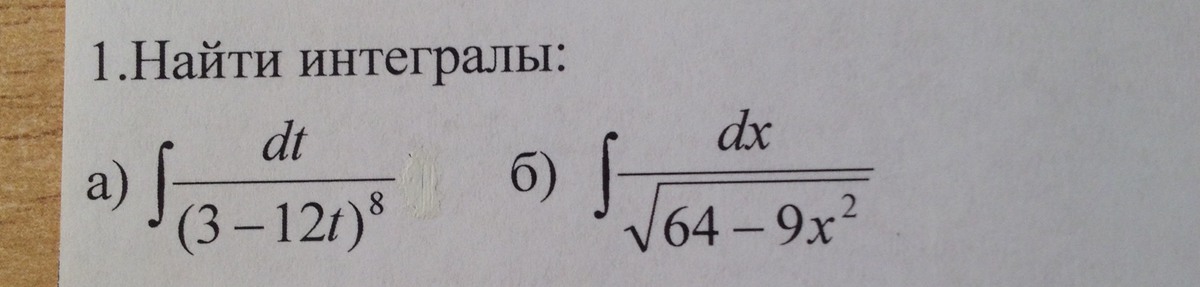
Ответы
Автор ответа:
1
Интегралы табличные, считаем методом замены переменной
(cм замены в квадратных скобках)
![\int{ \frac{dt}{(3-12t) ^{8} } } \, =[3-12t=u; -12dt=du; dt=- \frac{1}{12}du]= \\ \\ =- \frac{1}{12} \int{ \frac{du}{u ^{8} } } \, = - \frac{1}{12} \int{ u ^{-8 }du \, = - \frac{1}{12} \frac{u ^{-8+1} }{(-8+1)}+C= \\ \\ = \frac{1}{84u ^{7} }+C= \int{ \frac{dt}{(3-12t) ^{8} } } \, =[3-12t=u; -12dt=du; dt=- \frac{1}{12}du]= \\ \\ =- \frac{1}{12} \int{ \frac{du}{u ^{8} } } \, = - \frac{1}{12} \int{ u ^{-8 }du \, = - \frac{1}{12} \frac{u ^{-8+1} }{(-8+1)}+C= \\ \\ = \frac{1}{84u ^{7} }+C=](https://tex.z-dn.net/?f=+%5Cint%7B+%5Cfrac%7Bdt%7D%7B%283-12t%29+%5E%7B8%7D+%7D+%7D+%5C%2C+%3D%5B3-12t%3Du%3B+-12dt%3Ddu%3B+dt%3D-+%5Cfrac%7B1%7D%7B12%7Ddu%5D%3D+%5C%5C++%5C%5C+%3D-+%5Cfrac%7B1%7D%7B12%7D++%5Cint%7B+%5Cfrac%7Bdu%7D%7Bu+%5E%7B8%7D+%7D+%7D+%5C%2C++%3D+-+%5Cfrac%7B1%7D%7B12%7D++%5Cint%7B+u+%5E%7B-8+%7Ddu+%5C%2C++%3D+-+%5Cfrac%7B1%7D%7B12%7D++%5Cfrac%7Bu+%5E%7B-8%2B1%7D+%7D%7B%28-8%2B1%29%7D%2BC%3D+%5C%5C++%5C%5C+%3D+%5Cfrac%7B1%7D%7B84u+%5E%7B7%7D+%7D%2BC%3D)

![\int{ \frac{1}{ \sqrt{64-9 x^{2} } } } \, dx = \int{ \frac{1}{ \sqrt{8 ^{2} -(3 x)^{2} } } } \, dx =[3x=u; 3dx=du;dx= \frac{du}{3}]= \\ = \frac{1}{3} \int{ \frac{1}{ \sqrt{8 ^{2} -u^{2} } } } \, du= \frac{1}{3}arcsin \frac{u}{8}+C= \frac{1}{3}arcsin \frac{3x}{8}+C \int{ \frac{1}{ \sqrt{64-9 x^{2} } } } \, dx = \int{ \frac{1}{ \sqrt{8 ^{2} -(3 x)^{2} } } } \, dx =[3x=u; 3dx=du;dx= \frac{du}{3}]= \\ = \frac{1}{3} \int{ \frac{1}{ \sqrt{8 ^{2} -u^{2} } } } \, du= \frac{1}{3}arcsin \frac{u}{8}+C= \frac{1}{3}arcsin \frac{3x}{8}+C](https://tex.z-dn.net/?f=+%5Cint%7B+%5Cfrac%7B1%7D%7B+%5Csqrt%7B64-9+x%5E%7B2%7D+%7D+%7D+%7D+%5C%2C+dx+%3D+%5Cint%7B+%5Cfrac%7B1%7D%7B+%5Csqrt%7B8+%5E%7B2%7D+-%283+x%29%5E%7B2%7D+%7D+%7D+%7D+%5C%2C+dx+%3D%5B3x%3Du%3B+3dx%3Ddu%3Bdx%3D+%5Cfrac%7Bdu%7D%7B3%7D%5D%3D+%5C%5C+%3D++%5Cfrac%7B1%7D%7B3%7D++%5Cint%7B+%5Cfrac%7B1%7D%7B+%5Csqrt%7B8+%5E%7B2%7D+-u%5E%7B2%7D+%7D+%7D+%7D+%5C%2C+du%3D+%5Cfrac%7B1%7D%7B3%7Darcsin+%5Cfrac%7Bu%7D%7B8%7D%2BC%3D+%5Cfrac%7B1%7D%7B3%7Darcsin+%5Cfrac%7B3x%7D%7B8%7D%2BC)
(cм замены в квадратных скобках)
Похожие вопросы
Предмет: Другие предметы,
автор: Машенька432
Предмет: Русский язык,
автор: sevinchmuratova
Предмет: Українська мова,
автор: lizakestel
Предмет: Английский язык,
автор: limarenko202
Предмет: Математика,
автор: Faraon26