Предмет: Математика,
автор: 1892соня
Срочно нужно помогите 1)Средняя линия равностороннего треугольника ABC равна 11 см. Найдите периметр треугольника
2)К окружности с центром в точке О проведены касательная АВ и секущая АО Найдите радиус окружности, если АО=26 см, АВ=24 см.
Ответы
Автор ответа:
1
1) По свойствам средней линии - она параллельна одной из сторон
треугольника и равна половине этой стороны. Значит, сторона треугольника
равна 11*2=22 см. Треугольник равносторонний, все его стороны равны, значит, его периметр равен 22*3=66 см.
2) Обозначим точки пересечения секущей АО с окружностью как С и Д (см. рисунок). По теореме о касательной и секущей, если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть. Таким образом,
Пусть радиус СО равен х. Тогда АС=26-х, а AD=26+х
Подставив значения, получим:
576=(26-х)(26+х)


х=10
Радиус окружности равен 10 см.
2) Обозначим точки пересечения секущей АО с окружностью как С и Д (см. рисунок). По теореме о касательной и секущей, если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть. Таким образом,
Пусть радиус СО равен х. Тогда АС=26-х, а AD=26+х
Подставив значения, получим:
576=(26-х)(26+х)
х=10
Радиус окружности равен 10 см.
Приложения:
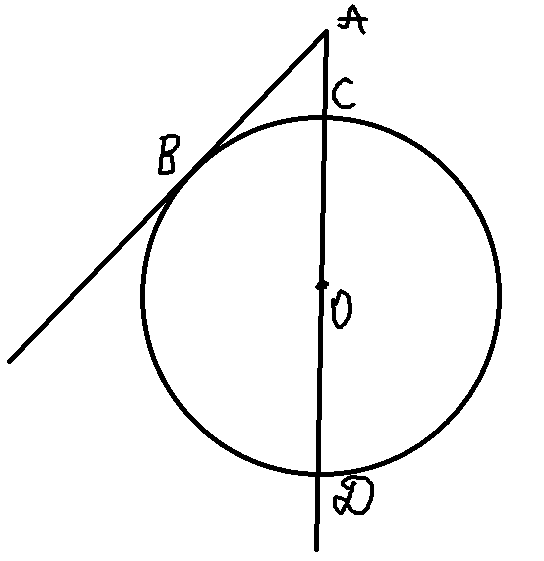
Похожие вопросы
Предмет: Русский язык,
автор: мафтуночка
Предмет: Қазақ тiлi,
автор: Fastuiop
Предмет: Окружающий мир,
автор: polina1249
Предмет: Математика,
автор: stmasusha