Предмет: Геометрия,
автор: mysterypeach23
Помогите срочно,пожалуйста
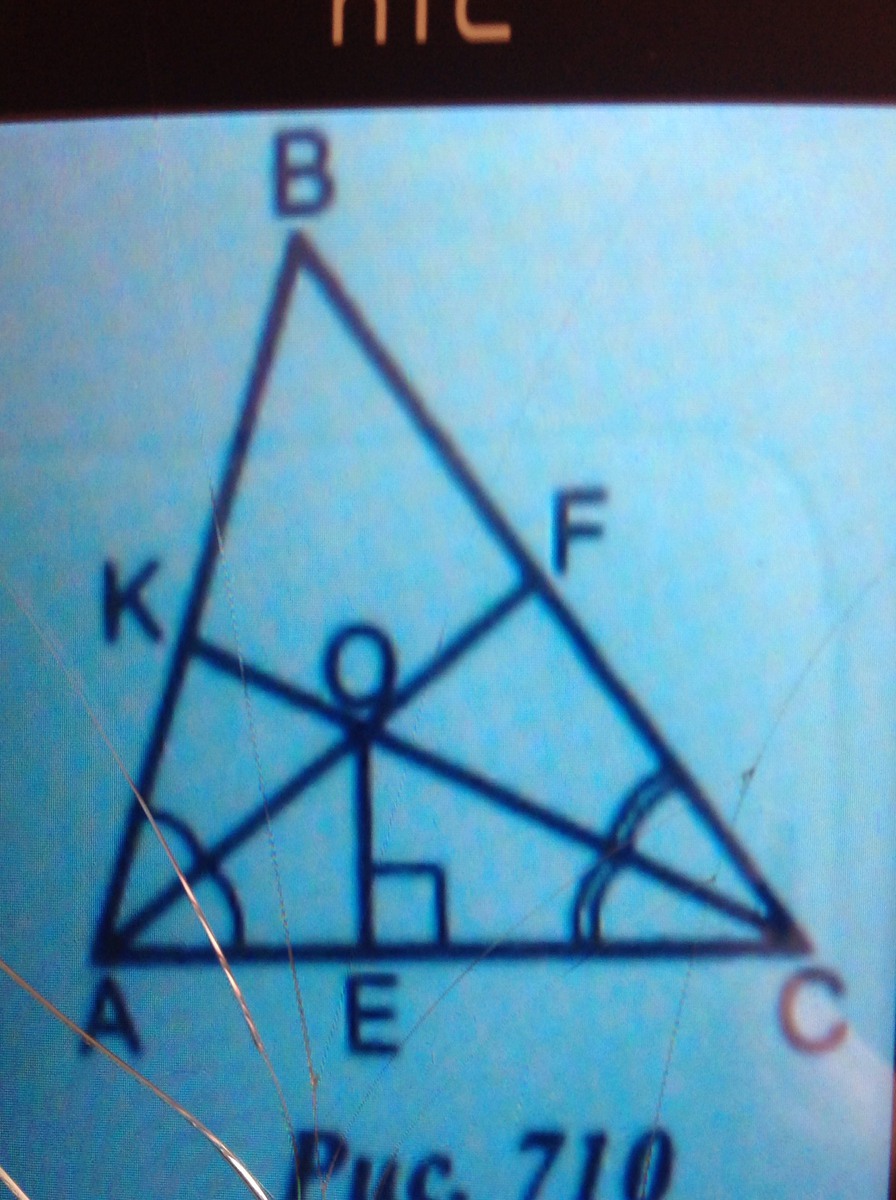
Рис. 110 дано:OE=5
Найти расстояние от точки О до прямых AB и BC
Приложения:
Катюша1007:
Тут не видно буквы внизу
внизу A E C
Ответы
Автор ответа:
14
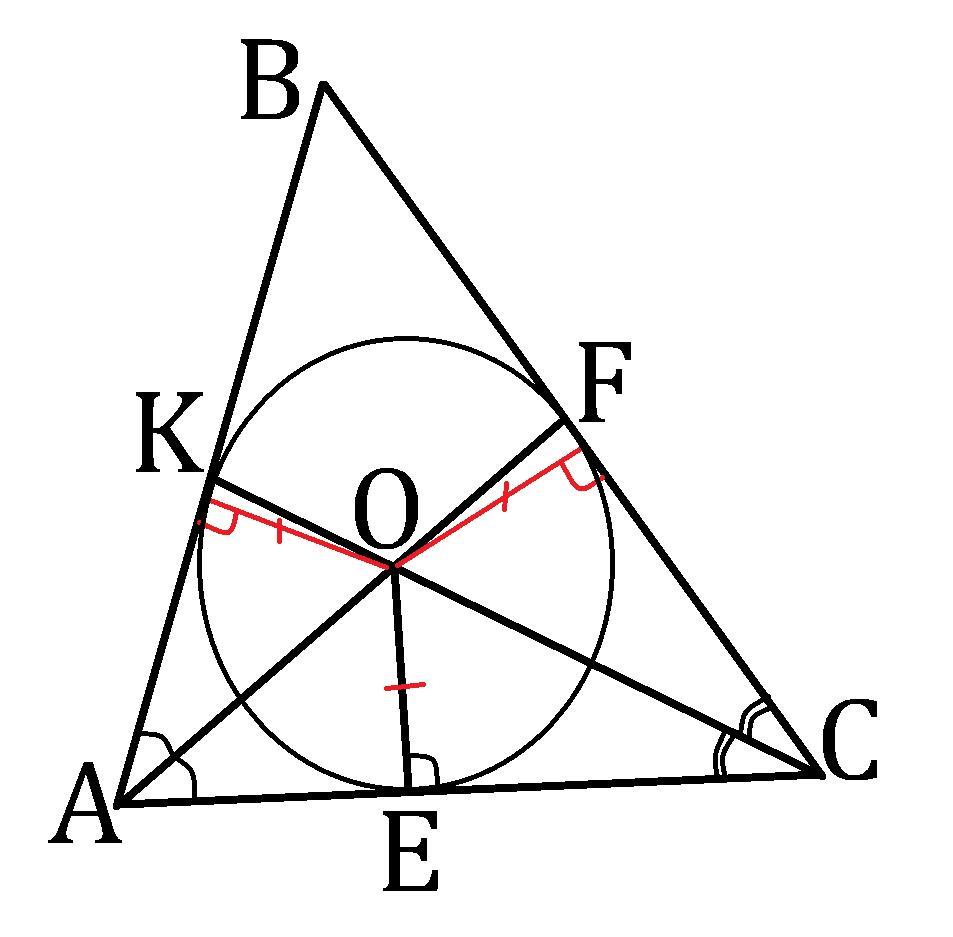
∠CAF=∠BAF ⇒ AF - биссектриса ∠CAB.
∠ACK=∠BCK ⇒ CK - биссектриса ∠BCA.
Центр вписанной окружности это точка пересечения биссектрис, AF∩CK=O ⇒ О - центр вписанной.
OE⊥AC и E∈AC ⇒ OE - радиус вписанной окружности.
Расстояние от центра вписанной до каждой стороны равно радиус этой окружности, поэтому d(O;AB) = d(O;BC) = OE = 5.
Ответ: оба расстояния равны 5.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: egsergen1
Предмет: Русский язык,
автор: Giyas2006
Предмет: Українська мова,
автор: max1zhurba
Предмет: Алгебра,
автор: wanjaka
Предмет: Русский язык,
автор: Iuliapoh