Question

Основание AC равнобедренного треугольника ABC равно 12. Окружность

радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC .

Answer 1

Вариант решения.
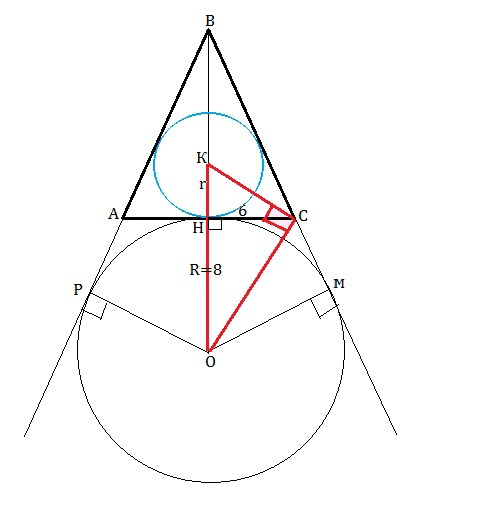
Пусть точки касания вневписанной окружности  с продолжениями сторон  АВ и ВС треугольника  АВС будут  Р и М.
Центр  О вписанной в угол окружности окружности лежит на его биссектрисе. 
СО - биссектриса угла АСМ, ВО - биссектриса угла РВМ.
Центр О лежит на их пересечении. 
Центр К вписанной в треугольник  ВСА окружности также лежит на пересечении его биссектрис ВН и СК. 
Центры вписанной и вневписанной окружностей лежат на одной прямой ВО как вписанные в один угол. 
Угол КСО - половина развернутного угла АСМ ( т.к. состоит из половин смежных углов). ⇒
Угол КСО=90°
Треугольник АВС - равнобедренный, ⇒ 
ВН его биссектриса, высота, медиана. ⇒
ВН перпендикулярна АС и делит её пополам.
АН=НС=12:2=6
Треугольник КСО - прямоугольный,
 СН - его высота, КО - гипотенуза. 
Высота прямоугольного треугольника, проведенная из прямого угла к биссектрисе, есть среднее пропорциональное отрезков, на которые делит её.
Отрезок КН = r = радиус вписанной окружности в треугольник АВС. 
Отрезок ОН=R=8 - радиус вневписанной окружности. 
СН²=КН*НО
36=r*8 ⇒
r=36:8=4,5
см. рисунок во вложении. 
-------
bzs@