Question

ПОМОГИТЕ ПОЖАЛУЙСТА ! ВЕК БУДУ БЛАГОДАРНА!!!

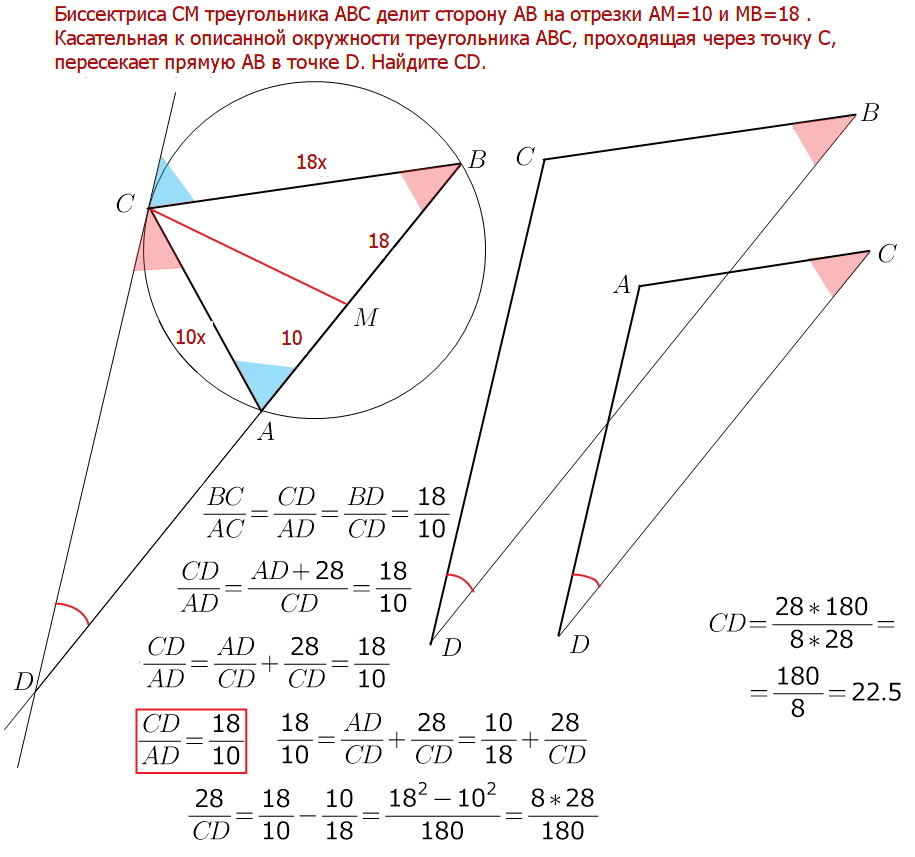
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18 . Касательная к описанной окружности треугольника ABC , проходящая через точку C , пересекает прямую AB в точке D . Найдите CD .

Answer 1

1) Биссектриса делит сторону на отрезки, пропорциональные прилежащим сторонам))) 18:10 = ВС:АС
2) если в задаче задано отношение сторон --нужно искать подобные треугольники...
3) Угол между касательной и секущей=половине градусной меры дуги, заключенной между касательной и секущей.
И вписанный в окружность угол=половине градусной меры дуги...
по двум равным углам нашли подобные треугольники, записали пропорцию...
DB=DA+AB=DA+28
если отношение СD:AD = 18:10,
то отношение AD:CD ---обратная величина... =10:18