Предмет: Геометрия,
автор: Аноним
Срочно, помогите пожалуйста!
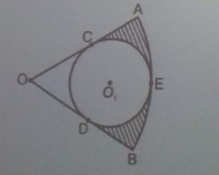
В сектор с центральным углом в 60° и радиусом, равным 6 см, вписана окружность. Найдите площадь заштрихованной фигуры изображённой на рисунке.
Приложения:
Ответы
Автор ответа:
36
Проведём 3 радиуса - ОЕ = R = 6 см, СО₁ и ДО₁ - это радиусы окружности r.
Угол СОО₁ = 60 / 2 = 30°, поэтому ОО₁ = 2r, а ОЕ = 3r.
Отсюда r = ОЕ / 3 = 6 / 3 = 2 см.
СО = 2r*cos 30° = 2*2*(√3/2) = 2√3 см.
Заштрихованная площадь равна площади сектора минус площадь сектора СЕД и минус площадь двух треугольников ОСО₁.
S = πR²*60 / 360 - πr²*240 / 360 -2*(1/2)*2*2√3 =
= π*6² / 6 - π2² / 3 - 8√3 = 6π -4π / 3 - 4√3 = (10π - 12√3) / 3 =
= 3,543772 см².
Угол СОО₁ = 60 / 2 = 30°, поэтому ОО₁ = 2r, а ОЕ = 3r.
Отсюда r = ОЕ / 3 = 6 / 3 = 2 см.
СО = 2r*cos 30° = 2*2*(√3/2) = 2√3 см.
Заштрихованная площадь равна площади сектора минус площадь сектора СЕД и минус площадь двух треугольников ОСО₁.
S = πR²*60 / 360 - πr²*240 / 360 -2*(1/2)*2*2√3 =
= π*6² / 6 - π2² / 3 - 8√3 = 6π -4π / 3 - 4√3 = (10π - 12√3) / 3 =
= 3,543772 см².
Похожие вопросы
Предмет: Окружающий мир,
автор: nigatevon
Предмет: Английский язык,
автор: Никита199511
Предмет: Английский язык,
автор: настякот2006
Предмет: Химия,
автор: XelenAr
Предмет: История,
автор: ncbfvbvvcv