Предмет: Алгебра,
автор: Таня476
Найдите число целых решений неравенства
Х в квадрате*3 в степени Х и вычесть 3 в степени Х+1 <=0
Приложения:
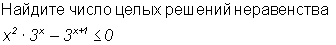
Ответы
Автор ответа:
0
9^x - 3^x - 6 > 0
3^2x - 3^x - 6 > 0
замена
3^x = y
ОДЗ: у > 0
y² - y - 6 > 0
найдём нули функции f(y) = y² - y - 6
решим уравнение y² - y - 6 = 0
D = 1 + 24 = 25
√D = 5
y₁ = (1 - 5):2 = -2
y₁ = (1 + 5):2 = 3
График функции f(y) = y² - y - 6 квадратная парабола веточками вверх, поэтому неравенство y² - y - 6 > 0 имеет решение у∈(-∞; -2)U (3; +∞)
c учётом ОДЗ получаем у∈(3; +∞)
вернёмся к замене
3^x = 3
х = 1
Ответ: х∈(1; +∞)
Похожие вопросы
Предмет: Русский язык,
автор: abdyvalievdmitri1911
Предмет: Литература,
автор: idrisovadzamila6
Предмет: Обществознание,
автор: spotifay20i20
Предмет: Литература,
автор: васяелмнгш