Предмет: Геометрия,
автор: leraol
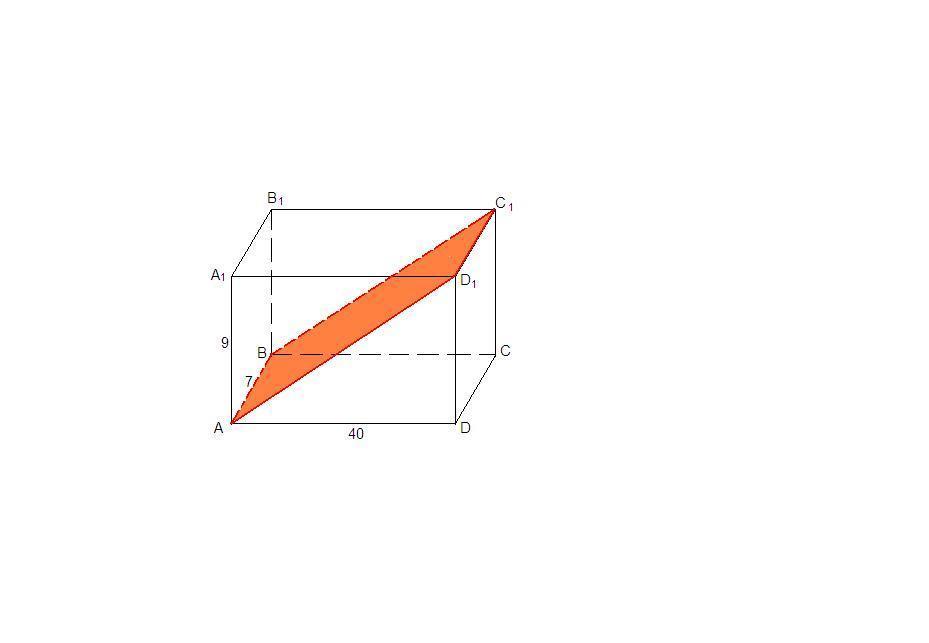
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=7?AD=40?AA1=9. Найдите площадь сечения параллелепипеда плоскостью,проходящей через точки A, B и C1
Ответы
Автор ответа:
5
Секущая плоскость пересекает параллельные грани по параллельным прямым.
Грань АВВ₁А₁ пересечена по прямой АВ.
В грани CDD₁C₁ через точку С₁ проходит прямая C₁D₁║АВ.
АВC₁D₁ - искомое сечение.
AD⊥AB так как все грани прямоугольники.
AD - проекция AD₁ на плоскость основания. ⇒
AD₁⊥AB, ⇒АВC₁D₁ - прямоугольник.
ΔAD₁D: ∠D = 90°, по теореме Пифагора
AD₁ = √(AD² + DD₁²) = √(1600 + 81) = √1681 = 41
Sabc₁d₁ = AB · AD₁ = 7 · 41 = 287
Грань АВВ₁А₁ пересечена по прямой АВ.
В грани CDD₁C₁ через точку С₁ проходит прямая C₁D₁║АВ.
АВC₁D₁ - искомое сечение.
AD⊥AB так как все грани прямоугольники.
AD - проекция AD₁ на плоскость основания. ⇒
AD₁⊥AB, ⇒АВC₁D₁ - прямоугольник.
ΔAD₁D: ∠D = 90°, по теореме Пифагора
AD₁ = √(AD² + DD₁²) = √(1600 + 81) = √1681 = 41
Sabc₁d₁ = AB · AD₁ = 7 · 41 = 287
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: zhannamerkulov
Предмет: Окружающий мир,
автор: dyadyadanya200oy4o3k
Предмет: Русский язык,
автор: AlinaSivaeva1
Предмет: История,
автор: LyckuDog
Предмет: Английский язык,
автор: Naazaar144