Предмет: Алгебра,
автор: kves
Решите тождество и 2 примера , пожалуйста .
Приложения:


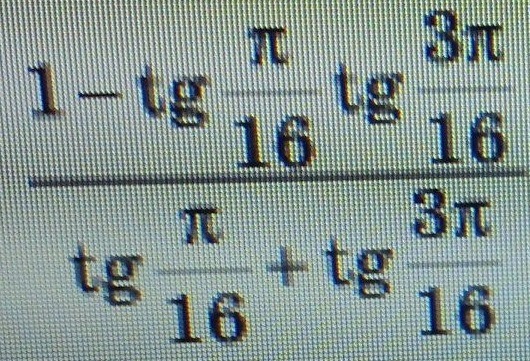
Ответы
Автор ответа:
1
tg55° - tg 35° = 



Аноним:
Вам не кажется, что во 2-м примере у Вас ошибка в преобразованиях (1 - cos α) : (1 + cos α)?
была, но я исправила
вижу. успехов!
Автор ответа:
1
1) tg 55 - tg 35 = 2tg 20
sin (55 - 35) : (cos 55 · cos 35) = 2tg 20
sin 20 : [0.5(cos (55 -35) + cos (55 + 35)] = 2tg 20
2sin 20 : (cos 20 + cos 90) = 2tg 20
2sin 20 : cos 20 = 2tg 20
2tg 20 ≡ 2tg 20
2) (2sin α - sin 2α) : (2sin α + sin 2α) =
= (2sin α - 2sin α ·cos α) : (2sin α + 2sin α · cos α) =
= [2sin α (1 - cos α)] : [2sin α (1 + cos α) =
= (1 - cos α) : (1 + cos α) =
= 2sin² 0.5α : 2cos² 0.5α =
= 2tg² 0.5α
3) 1 - tg π/16 · tg 3π/16) : (tg π/16 + tg 3π/16) =
= (tg π/16 + tg 3π/16) : [(tg π/16 + tg 3π/16) · tg (π/16 + 3π/16) =
= 1 : tg 4π/16 = 1 : tg π/4 = 1 : 1 = 1
sin (55 - 35) : (cos 55 · cos 35) = 2tg 20
sin 20 : [0.5(cos (55 -35) + cos (55 + 35)] = 2tg 20
2sin 20 : (cos 20 + cos 90) = 2tg 20
2sin 20 : cos 20 = 2tg 20
2tg 20 ≡ 2tg 20
2) (2sin α - sin 2α) : (2sin α + sin 2α) =
= (2sin α - 2sin α ·cos α) : (2sin α + 2sin α · cos α) =
= [2sin α (1 - cos α)] : [2sin α (1 + cos α) =
= (1 - cos α) : (1 + cos α) =
= 2sin² 0.5α : 2cos² 0.5α =
= 2tg² 0.5α
3) 1 - tg π/16 · tg 3π/16) : (tg π/16 + tg 3π/16) =
= (tg π/16 + tg 3π/16) : [(tg π/16 + tg 3π/16) · tg (π/16 + 3π/16) =
= 1 : tg 4π/16 = 1 : tg π/4 = 1 : 1 = 1
Похожие вопросы
Предмет: Українська мова,
автор: Nik12375
Предмет: Русский язык,
автор: коко61
Предмет: Окружающий мир,
автор: pro335
Предмет: Физика,
автор: Вайллет