докажите теорему что все точки каждой из двух параллельных прямых равноудалены от другой прямой
Ответы
Расстояние между двумя параллельными прямыми есть длина перпендикуляра, опущенного из некой точки одной прямой на другую.
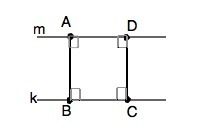
. Пусть даны параллельные прямые m и k
Возьмём на прямой m произвольную точку А и проведем через неё перпендикуляр до пересечения с прямой k в точке В
Так как если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой, то углы, образованные отрезком АВ - и прямыми m и k - прямые.
Таким же образом выберем на некотором расстоянии от т.А точку D и проведем через неё перпендикуляр DC, который образует с прямыми m и k прямые углы.
Четырёхугольник АВСD- прямоугольник (все углы прямые). Так как в прямоугольнике противоположные стороны равны, АВ=СD, т.е точки А и D на прямой m равноудалены от прямой k. =>
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
-------------
Существуют и другие доказательства. Попробуйте найти их самостоятельно.