Предмет: Алгебра,
автор: Jully555
Алгебра. Алимов 10-11 класс. Блок проверь себя на странице 311 №4
Приложения:
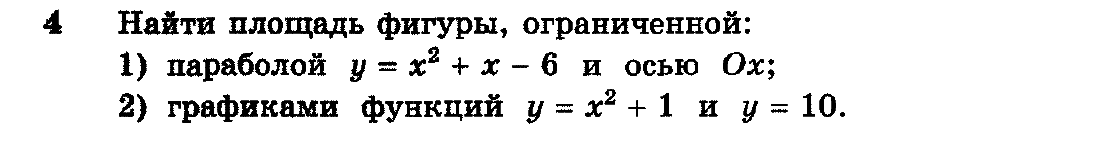
Ответы
Автор ответа:
14
1) Площадь фигуры находится через интеграл.
Найдем пределы интегрирования:




2)


Найдем пределы интегрирования:
2)
Похожие вопросы
Предмет: Русский язык,
автор: karinaahoran
Предмет: Английский язык,
автор: aidana9810
Предмет: Русский язык,
автор: Fauzen2
Предмет: Математика,
автор: katy228226
Предмет: География,
автор: latypovislam299