в параллелограмме abcd биссектриса острого угла равного 60 градусов, делит сторону параллелограмма на отрезки 25 и 15 см, начиная от вершины тупого угла.найдите биссектрису и меньшую диагональ параллелограмма
Ответы
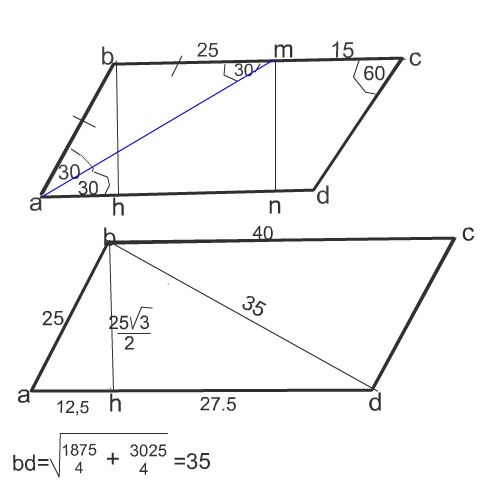
Сделаем рисунок к задаче.
Примем во внимание, что ∠ abd совсем не обязательно должен быть равен 90°, и на самом деле он не 90°, хотя и похож, потому при решении проигнорируем его.
Треугольник abm- равнобедренный.
В нем ∠ amb=∠ mad как углы при пересечении параллельных прямых секущей, а
∠ bam=∠ mad по построению.
Опустим из вершины b высоту bh.
ah=ab·sin(30)=25·1/2=12,5
bh=ab*sin(60)=(25√3):2
hd=(25+15)-12,5=27,5
bd= √(bh²+hd²)=√(25√3):2)²+(27,5 )²= √(1875/4+3025/4)=√4900/4=35 см
( можно и по теореме косинусов, результат должен быть одинаковым)
mn=bh=(25√3):2
Рассмотрим ᐃ amn
mn противолежит углу 30 градусов.
отсюда биссектриса am=2 mn=2·(25√3):2=25√3
Меньшая диагональ параллеограмма
bd= √ =35 см
Биссектриса
mn= 25√3 см
------------------
Провертьте мои вычисления меньшей диагонали для полной уверенности.