Предмет: Алгебра,
автор: Аноним
Решим подробненько)
Задание в приложении
Приложения:
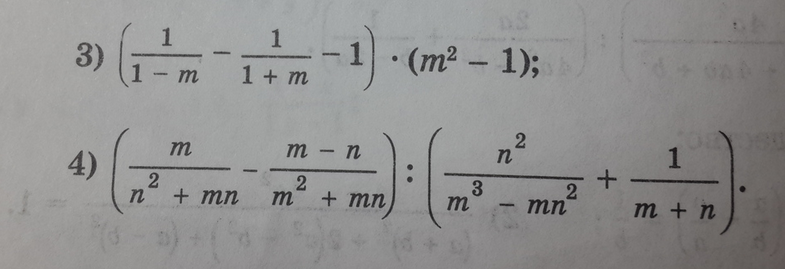
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: taylakova090820
Предмет: Окружающий мир,
автор: kotikuchenik
Предмет: Русский язык,
автор: аххаха2
Предмет: Геометрия,
автор: valera228salman
Предмет: Алгебра,
автор: Аноним