Question

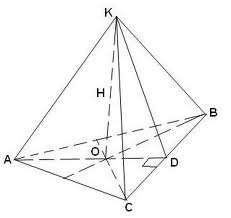
в правильной треугольной пирамиде боковое ребро равно 4√2 и образовывает угол 45 градусов с плоскостью основания. найти объем пирамиды.

Answer 1

угол КВО=45

1.рассмотрим треугольник КВО: прямоугольный

угол ОКВ=90-45=45, следовательно треугольник КВО - равнобедренный, следовательно ОВ=ОК
2.Пусть ОВ=х, то ОК=х
OB^2 + OK^2=KB^2 (по теореме пифагора)
x^2+x^2=32
2x^2=32
x^2=16
x=4(см) =ОВ=OK
3.ОВ - радиус описанной около основания окружности( R)
R=a/√3, а=R*√3 = 4√3 см
4. S осн =(а^2 *√3 ) /4 = 12 √3(cm^2)
5. V=1/3 * Sосн * H= 1/3 * S ocn * KO = 1/3 * 12√3*4 = 16√3 (cm^3)

 

 

 

 

Answer 2

Решение во вложении+ чертеж.

d7a4ab1796d6d56dd7a216b7b5117275.doc