Предмет: Геометрия,
автор: belkovan
Пожалуйста помогите
Конус, радиус основания которого равен 15 дм, а высота 20 дм, имеет общее основание с полушаром. Найдите площадь поверхности полушара, находящейся: а) внутри конуса
Ответы
Автор ответа:
1
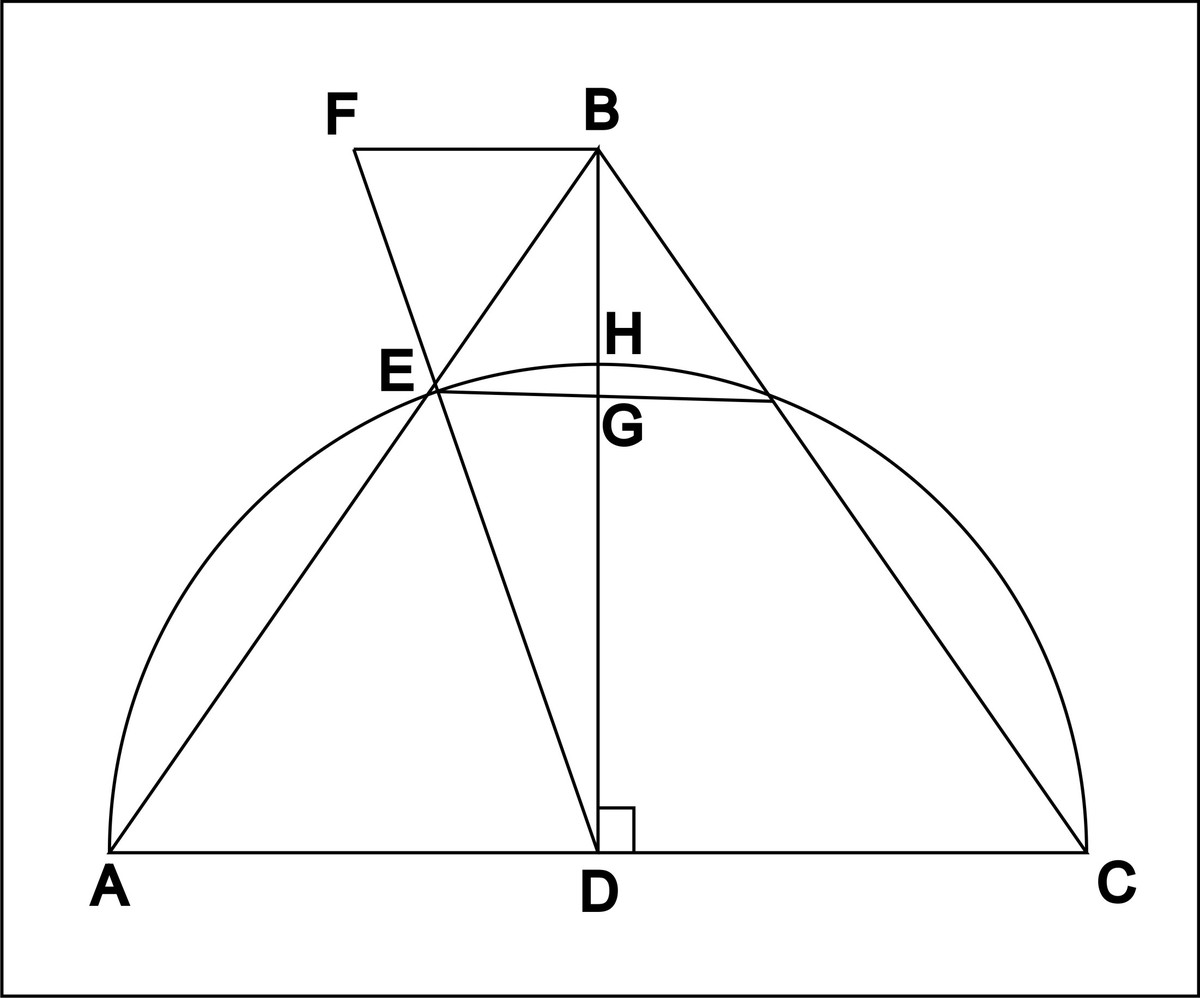
ABC-осевое сечение конуса
AD=DE=15
BD=20
по теореме Пифагора
AB=25
треугольники FBE и EDA подобны
FB/AD=FE/ED
тк AD=ED то FB=FE
запишем теорему Пифагора для треугольника FBD
FB^2+BD^2=(FE+ED)^2
FB^2+400=(FB+15)^2
FB=35/6
из подобия треугольников FBE и EAD получаем
AE/ED=18/7
DG/GB=18/7
DG+GB=20
GB=28/5
HG=3/5 - высота сегмента шара, находящегося внутри конуса
S=2пRH=2п*15*(3/5)=18п
AD=DE=15
BD=20
по теореме Пифагора
AB=25
треугольники FBE и EDA подобны
FB/AD=FE/ED
тк AD=ED то FB=FE
запишем теорему Пифагора для треугольника FBD
FB^2+BD^2=(FE+ED)^2
FB^2+400=(FB+15)^2
FB=35/6
из подобия треугольников FBE и EAD получаем
AE/ED=18/7
DG/GB=18/7
DG+GB=20
GB=28/5
HG=3/5 - высота сегмента шара, находящегося внутри конуса
S=2пRH=2п*15*(3/5)=18п
Приложения:
tolya91:
блин я болел плохо себя чувстовал поэтому не решал. но если чё можешь обращаться
С Выздоровлением )))
спасибо)
здравствуйте помогите мне пожалуйста)
#34.45. Найдите все положительные значения параметра а, при которых неравенство |2х + a|x| - 13| > 1 выполняется для всех х из отрезка [-3; 3].
пожалуйста
пытаюсь решить
получаеться ?
почти) щас, скоро напишу решение
я отправил
Похожие вопросы
Предмет: Русский язык,
автор: emeraldm
Предмет: Қазақ тiлi,
автор: сармановафакизат
Предмет: Английский язык,
автор: klikliar
Предмет: Математика,
автор: marip19
Предмет: Английский язык,
автор: Зазнайка154