Предмет: Алгебра,
автор: wollex
Решить иррациональное неравенство
Приложения:
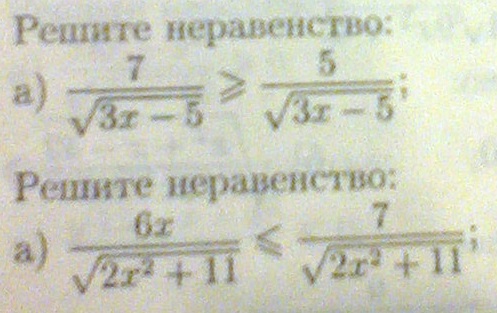
Ответы
Автор ответа:
1
а)
как корень в знаменателе, поэтому при сокращении на это выражение знак неравенства сохранится, но надо помнить об условии существовании этого выражения.
Ответ:
б)
Сократим аналогично предыдущему пункту. Сокращаем мы потому, что выражения абсолютно одинаковы и не влияют на знак неравенства.
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: Totiva
Предмет: Русский язык,
автор: VanyaByr06
Предмет: Русский язык,
автор: arushambaryan1
Предмет: Физика,
автор: StefanSalvatori
Предмет: Русский язык,
автор: Аноним