Предмет: Геометрия,
автор: shur729
радиус сферы вписанной в правильную четырехугольную пирамиду равен 3см, а длина диагонали ее основания -12√2 см. высислите обьем пирамиды.
Ответы
Автор ответа:
0
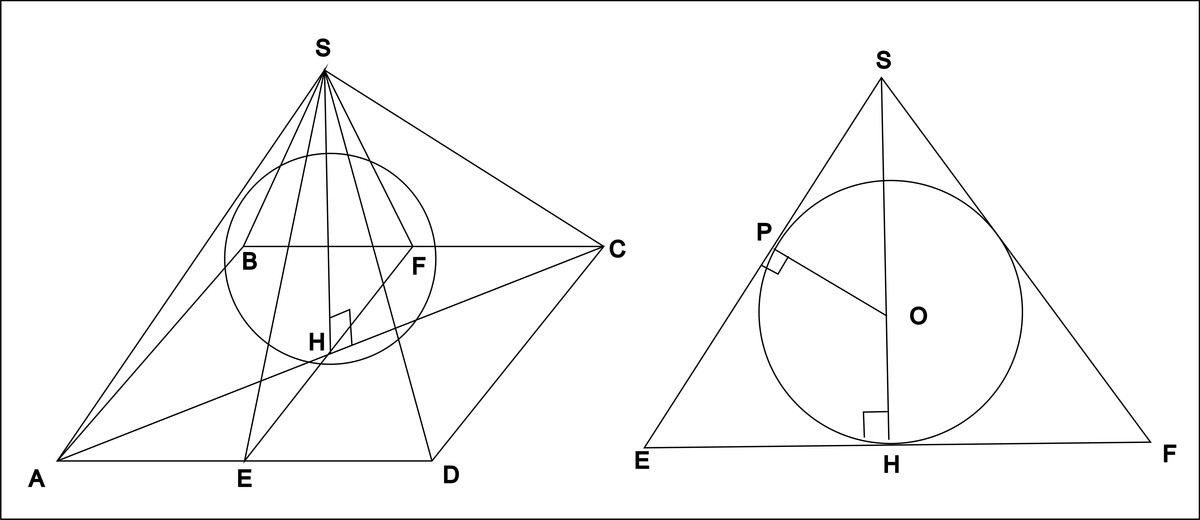
по теореме Пифагора
EH^2+AE^2=AH^2
EH=AE, тк НАЕ=45
EH=6
рассмотрим сечение SEF
OP=3
по теореме Пифагора
SE^2=SH^2+EH^2
из подобия треугольников SPO и SHE
PO/EH=SO/SE
3/6=(SH-3)/sqrt{x^2+36}
SH=8
SH-высота пирамиды
Объём пирамиды находится по формуле V=(1/3)*H*S
где Н-высота пирамиды, S-площадь основания
V=(1/3)*8*12*12=384
EH^2+AE^2=AH^2
EH=AE, тк НАЕ=45
EH=6
рассмотрим сечение SEF
OP=3
по теореме Пифагора
SE^2=SH^2+EH^2
из подобия треугольников SPO и SHE
PO/EH=SO/SE
3/6=(SH-3)/sqrt{x^2+36}
SH=8
SH-высота пирамиды
Объём пирамиды находится по формуле V=(1/3)*H*S
где Н-высота пирамиды, S-площадь основания
V=(1/3)*8*12*12=384
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: serebrova04live
Предмет: Русский язык,
автор: evgosha1
Предмет: Русский язык,
автор: влад20491
Предмет: Українська література,
автор: 567390765
Предмет: Математика,
автор: эпик154