Предмет: Геометрия,
автор: sunnykonchenko
Решите пожалуйста . Стороны угла А касаются окружности с центром О радиуса r. Найдите: б) r, если ОА = 14 дм, угол а = 90 градусов.
Ответы
Автор ответа:
1
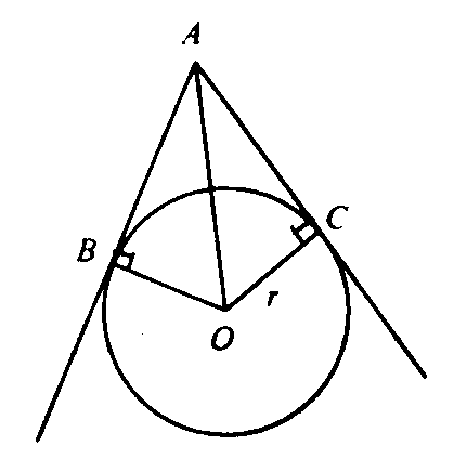
Дано: AB, AC - касательные к Окр (О;r),АО=14,угол А=90, r-?
OB перпендикулярен АВ,OC перпендикулярен АС =>AO является биссектрисой.Рассмотрим треугольник АОС,где угол С=90,т.к АО-биссектриса,она делит пополам угол А,значит в треугольник угол А равен 90/2=45.Получили равнобедренный прямоугольный треугольник.
пусть ОС=АС=х,тогда по теореме пифагора найдем
АО^2=OC^2+AC^2
AO^2=2x^2
196=2x^2
x=
Ответ:r=
OB перпендикулярен АВ,OC перпендикулярен АС =>AO является биссектрисой.Рассмотрим треугольник АОС,где угол С=90,т.к АО-биссектриса,она делит пополам угол А,значит в треугольник угол А равен 90/2=45.Получили равнобедренный прямоугольный треугольник.
пусть ОС=АС=х,тогда по теореме пифагора найдем
АО^2=OC^2+AC^2
AO^2=2x^2
196=2x^2
x=
Ответ:r=
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: liza0916
Предмет: Английский язык,
автор: darecome08
Предмет: Английский язык,
автор: vana2233
Предмет: Английский язык,
автор: showshmel