Предмет: Алгебра,
автор: locer
РЕШИТЕ УРАВНЕНИЯ
и покажите решение
Приложения:
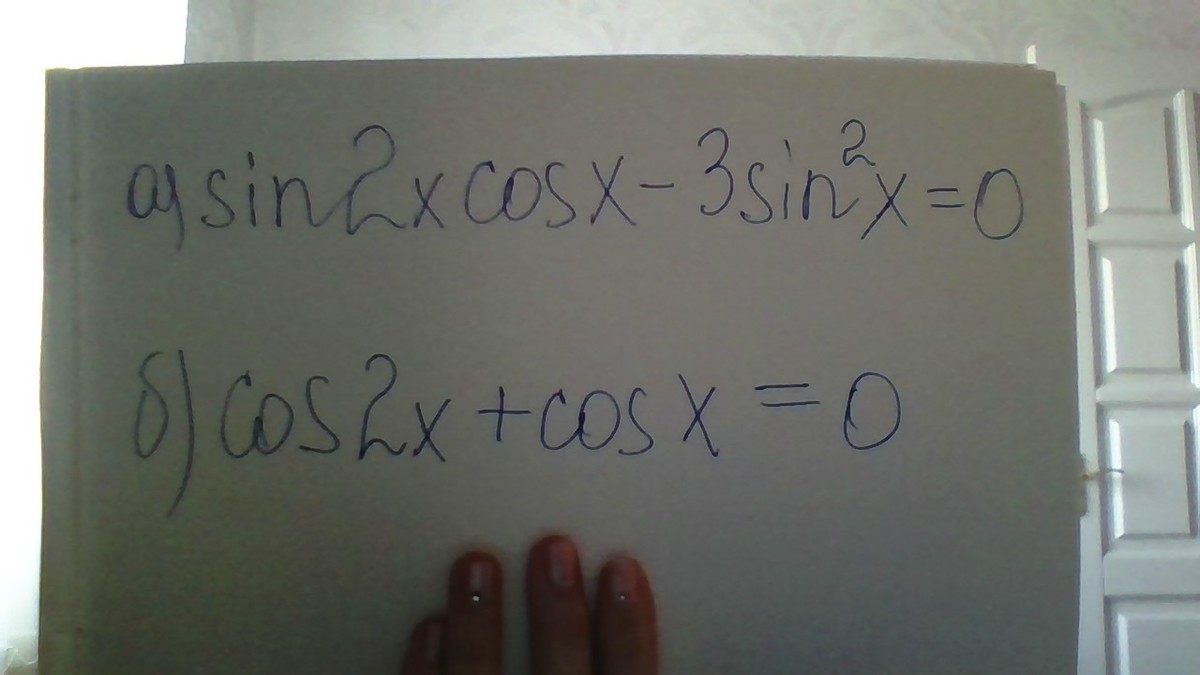
Ответы
Автор ответа:
1
а) sin 2x*cos x - 3sin^2 x = 0
2sin x*cos x*cos x - 3sin^2 x = 0
sin x*(2cos^2 x - 3sin x) = 0
1) sin x = 0, x1 = pi*k
2) 2cos^2 x - 3sin x = 2(1 - sin^2 x) - 3sin x = 0
2sin^2 x + 3sin x - 2 = 0
Квадратное уравнение относительно sin x
(2sin x - 1)(sin x + 2) = 0
sin x = 1/2, x2 = (-1)^n*pi/6 + pi*n
sin x = -2 - решений нет
б) cos 2x + cos x = 0
2cos^2 x - 1 + cos x = 0
Квадратное уравнение относительно cos x
(cos x + 1)(2cos x - 1) = 0
cos x = -1, x1 = pi + 2pi*k
cos x = 1/2, x2 = +-pi/3 + 2pi*n
2sin x*cos x*cos x - 3sin^2 x = 0
sin x*(2cos^2 x - 3sin x) = 0
1) sin x = 0, x1 = pi*k
2) 2cos^2 x - 3sin x = 2(1 - sin^2 x) - 3sin x = 0
2sin^2 x + 3sin x - 2 = 0
Квадратное уравнение относительно sin x
(2sin x - 1)(sin x + 2) = 0
sin x = 1/2, x2 = (-1)^n*pi/6 + pi*n
sin x = -2 - решений нет
б) cos 2x + cos x = 0
2cos^2 x - 1 + cos x = 0
Квадратное уравнение относительно cos x
(cos x + 1)(2cos x - 1) = 0
cos x = -1, x1 = pi + 2pi*k
cos x = 1/2, x2 = +-pi/3 + 2pi*n
Похожие вопросы
Предмет: Русский язык,
автор: NASTYA2648234
Предмет: Английский язык,
автор: vulpe
Предмет: Українська література,
автор: Nipii
Предмет: Қазақ тiлi,
автор: manch26
Предмет: Математика,
автор: Markshne