Предмет: Математика,
автор: Valya74
Решите тригонометрическое уравнение
Приложения:
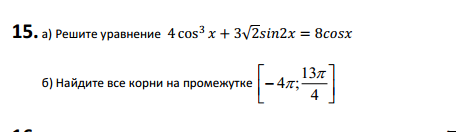
Ответы
Автор ответа:
1
Дополнительные формулы:

***************************************

Произведение равно нулю

Пусть , тогда получаем
, тогда получаем

находим дискрминант


 - не удовлетворяет условие при
- не удовлетворяет условие при 
Возвращаемся к замене

Отбор корней
Для корня

Для корня

***************************************
Произведение равно нулю
Пусть
находим дискрминант
Возвращаемся к замене
Отбор корней
Для корня
Для корня
Похожие вопросы
Предмет: Українська мова,
автор: Ritusik1
Предмет: Українська мова,
автор: lizonakravchen
Предмет: Английский язык,
автор: лисЯр
Предмет: Английский язык,
автор: Kewapar
Предмет: Алгебра,
автор: LittleCat666