Question

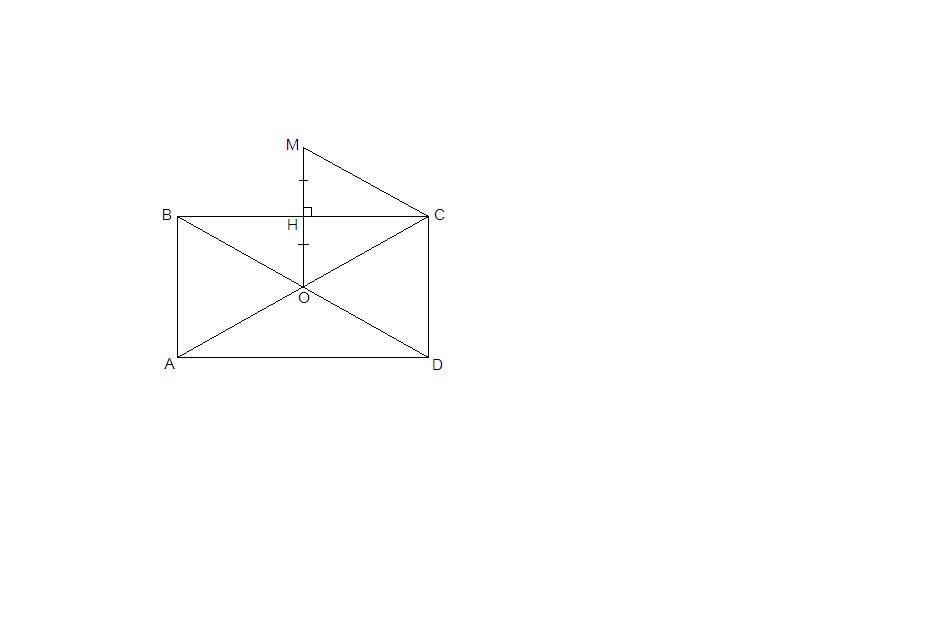
ПОМОГИТЕ !!!!МНОГО БАЛЛОВ 1) Дан прямоугольник ABCD, O - точка пересечения его диагоналей. Точка M симметрична точке O относительно стороны BC. Докажите,что четырехугольник MODC


- параллелограмм. Найдите его периметр,если стороны прямоугольника 6 см и 8 см.

Answer 1

Чтобы построить точку М, симметричную точке О относительно ВС, проведем луч с началом в точке О перпендикулярно ВС. Пусть Н - точка пересечения этого луча со стороной ВС. Отложим на луче отрезок НМ, равный отрезку ОН. Точка М построена.
OM║CD как перпендикуляры к одной прямой. О - середина BD ⇒
ОН  средняя линия ΔCBD. ОН = CD/2 = 3 cм.
НМ = ОН = 3 см по построению.
Итак, OM║CD, OM = CD ⇒MОDС - параллелограмм.

ΔABD: ∠A = 90°, по теореме Пифагора
BD = √(AB² + AD²) = √(64 + 36) = √100 = 10 (см)
OD = BD/2 = 5 см
Рmodc = 2(OD + DC) = 2(5 + 6)  = 22 см