В треугольнике ABC угол A в 4 раза меньше угла B, а угол C на 90 градусов меньше угла B
а) НАЙДИТЕ УГЛЫ ТРЕУГОЛЬНИКА
б) СРАВНИТЕ СТОРОНЫ AB и BC.
Ответы
В Δ ABC угол A в 4 раза меньше угла B ⇒ ∠B = 4∠A
В Δ ABC угол C на 90° меньше угла B ⇒ ∠C = ∠B - 90° ⇒ ∠C = 4∠A - 90°
Сумма углов треугольника равна 180°
∠A + ∠B + ∠C = 180°
∠A + 4∠A + 4∠A - 90° = 180°
9∠A = 270° ⇒ ∠A = 30°
∠B = 4∠A = 4*30° = 120°; ∠B = 120°
∠C = ∠B - 90° = 120° - 90° = 30°; ∠C = 30°
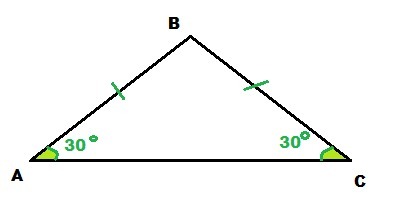
Сторона АВ лежит напротив ∠С = 30°
Сторона ВС лежит напротив ∠А = 30°
Так как углы равны, значит, и стороны против этих углов в треугольнике равны : АВ = ВС
Ответ: ∠А = ∠С = 30°; ∠В = 120°; АВ = ВС
Сумма углов треугольника равна 180°.
Пусть ∠А = х°, тогда ∠В = (4х)°, а ∠С = (4х - 90)°. Срставим и решим уравнение
х + 4х + 4х - 90 = 180,
9х = 180 + 90,
9х = 270,
х = 270 : 9,
х = 30.
Значит, ∠А = 30°, ∠В = 4 · 30° = 120°, ∠С = 120° - 90° = 30°.
Против ∠А лежит сторона ВС, АВ лежит против ∠С.
Теорема. Против большего угла треугольника лежит большая сторона.
Теорема. Против большей стороны лежит больший угол.
Т.к. ∠А = ∠С = 30°, то и АВ = ВС.
Ответ: а) 30°, 120° и 30°; б) равны.