Предмет: Алгебра,
автор: gjycfxfcgnjkjj
sin^2(x)-2sin(x)*cos(x)-3cos^2(x)+2=0
Ответы
Автор ответа:
1
Вроде бы так с::
Решение на картинке с:
Решение на картинке с:
Приложения:
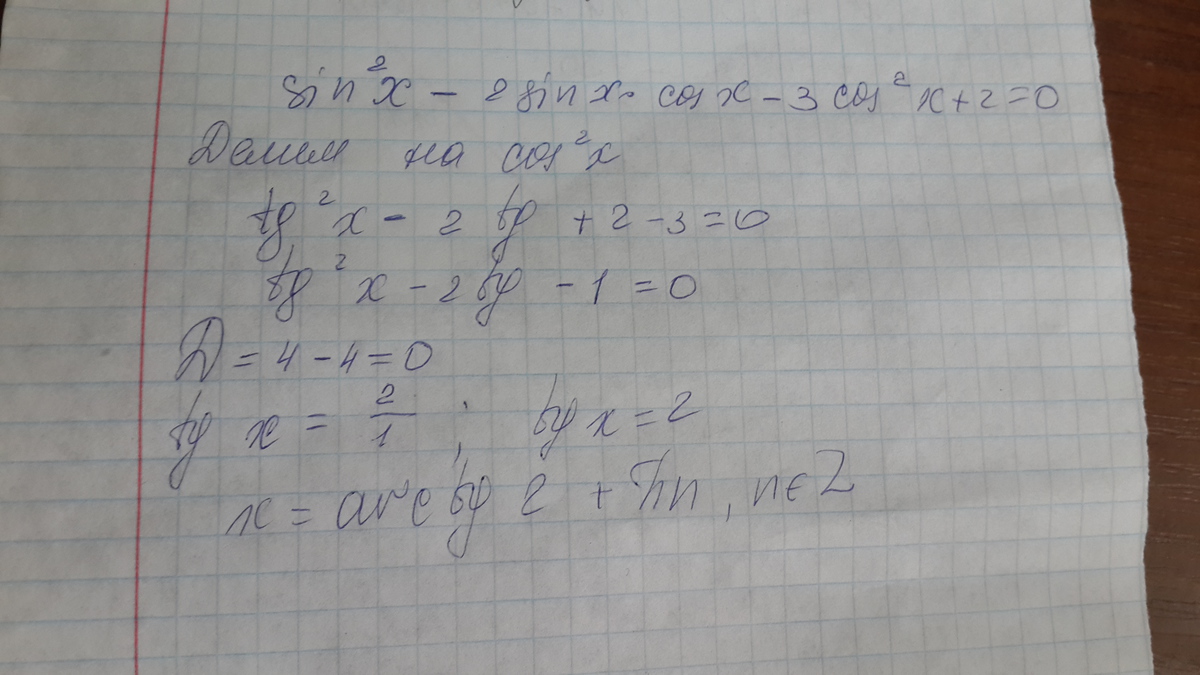
CrazyEch:
Черт, кажется у меня не правильно :с
Автор ответа:
1
Поскольку sin²x+cos²x=1


Делим выражение на cos²x
3tg²x-2tgx-1=0
tgx=1, tg=-
x=arctg1+πn, где n∈Z или x=-arctg +πn, где n∈Z
+πn, где n∈Z
x= +πn, где n∈Z
+πn, где n∈Z
Делим выражение на cos²x
3tg²x-2tgx-1=0
tgx=1, tg=-
x=arctg1+πn, где n∈Z или x=-arctg
x=
откуда в конце первой строки взялось "2sin^2(x)+2cos^2x"?
Это так двойку представили по тригонометрическому тождеству
1=sin^2+cos^2
Похожие вопросы
Предмет: Русский язык,
автор: Varenik2005
Предмет: Русский язык,
автор: СтарыйМудрец12
Предмет: Английский язык,
автор: lerka52781
Предмет: Українська мова,
автор: Аноним
Предмет: История,
автор: schoolboy30